ГДЗ по Геометрии 10 класс Номер 67 Атанасян — Подробные Ответы

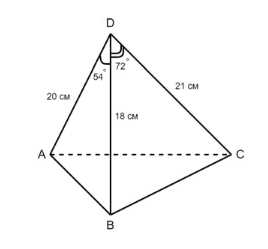
В тетраэдре \(DABC\) дано: \(L_{ADB}=54°\), \(Z_{BDC}= 72°\), \(L_{CDA}=90°\), \(DA = 20\) см, \(BD = 18\) см, \(DC = 21\) см. Найдите: а) рёбра основания \(ABC\) данного тетраэдра; б) площади всех боковых граней.

Для нахождения ребер основания \(ABC\) тетраэдра \(DABC\) воспользуемся теоремой косинусов:
\(a^2 = b^2 + c^2 — 2bc\cos A\), \(b^2 = a^2 + c^2 — 2ac\cos B\),
\(c^2 = a^2 + b^2 — 2ab\cos C\).
Подставляя известные данные, получаем:
\(a \approx 17.9\) см, \(b \approx 24.1\) см, \(c = 2\) см

Для нахождения площадей боковых граней используем формулу: \[S = \frac{1}{2}ab\sin C\]. Площади граней: \(S_{ADB} \approx 144\) см\(^2\), \(S_{BDC} \approx 180\) см\(^2\), \(S_{CDA} = 210\) см\(^2\)

Решение:

Для нахождения ребер основания \(ABC\) тетраэдра \(DABC\) воспользуемся теоремой косинусов:

\(a^2 = b^2 + c^2 — 2bc\cos A\)
\(b^2 = a^2 + c^2 — 2ac\cos B\)
\(c^2 = a^2 + b^2 — 2ab\cos C\)

Где \(a\), \(b\), \(c\) — длины сторон треугольника \(ABC\), а \(A\), \(B\), \(C\) — соответствующие углы.

Подставляя известные данные:
\(a^2 = 18^2 + 21^2 — 2\cdot18\cdot21\cos54° = 324 + 441 — 756\cdot0.588 = 765 — 444=\)
\( = 321\)
\(a = \sqrt{321} \approx 17.9\text{ см}\)

\(b^2 = 20^2 + 21^2 — 2\cdot20\cdot21\cos72° = 400 + 441 — 840\cdot0.309 = 841 — 259 = \)
\( = 582\)
\(b = \sqrt{582} \approx 24.1\text{ см}\)

\(c^2 = 20^2 + 18^2 — 2\cdot20\cdot18\cos90° = 400 + 324 — 720 = 4\)
\(c = 2\text{ см}\)

Таким образом, ребра основания \(ABC\) равны:
\(AB \approx 17.9\) см, \(BC \approx 24.1\) см, \(AC = 2\) см.

Для нахождения площадей боковых граней используем формулу:
\(S = \frac{1}{2}ab\sin C\)

Площадь грани \(ADB\):
\(S_{ADB} = \frac{1}{2}\cdot20\cdot18\sin54° \approx 144\text{ см}^2\)

Площадь грани \(BDC\):
\(S_{BDC} = \frac{1}{2}\cdot18\cdot21\sin72° \approx 180\text{ см}^2\)

Площадь грани \(CDA\):
\(S_{CDA} = \frac{1}{2}\cdot20\cdot21\sin90° = 210\text{ см}^2\)

Таким образом, найдены все необходимые параметры тетраэдра \(DABC\).