
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 66 Атанасян — Подробные Ответы
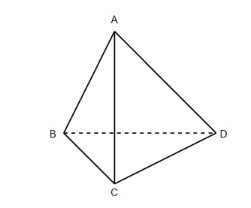
Назовите все пары скрещивающихся (т. е. принадлежащих скрещивающимся прямым) рёбер тетраэдра \(ABCD\). Сколько таких пар рёбер имеет тетраэдр?
Согласно условию задачи, скрещивающимися рёбрами тетраэдра \(ABCD\) являются:
\(AC, BD\)
\(AB, CD\)
\(AD, BC\)
Таким образом, в тетраэдре \(ABCD\) имеется 3 пары скрещивающихся рёбер.
Скрещивающимися прямыми называются прямые, которые не лежат в одной плоскости. Для тетраэдра \(ABCD\) это означает, что ребра, принадлежащие скрещивающимся прямым, также не лежат в одной грани тетраэдра.
Чтобы найти все пары скрещивающихся рёбер, нужно проанализировать, какие ребра тетраэдра не принадлежат одной грани. Из рисунка видно, что таких пар рёбер три:
1. \(AC\) и \(BD\) — эти ребра не лежат в одной грани тетраэдра, поэтому они образуют пару скрещивающихся рёбер.
2. \(AB\) и \(CD\) — эти ребра также не принадлежат одной грани, следовательно, они тоже образуют пару скрещивающихся рёбер.
3. \(AD\) и \(BC\) — эти ребра не лежат в одной грани тетраэдра, поэтому они составляют третью пару скрещивающихся рёбер.
Таким образом, в тетраэдре \(ABCD\) имеется 3 пары скрещивающихся рёбер: \((AC, BD), (AB, CD), (AD, BC)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!