
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 65 Атанасян — Подробные Ответы
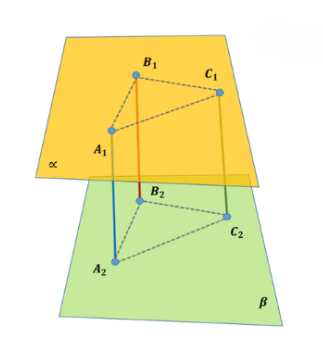
Параллельные отрезки \(A_1A_2\), \(B_1B_2\) и \(C_1C_2\) заключены между параллельными плоскостями \(a\) и \(B\) (рис. 32)
а) Определите вид четырёхугольников \(A_1B_1B_2A_2\), \(B_1C_1C_2B_2\) и \(A_1C_1C_2A_2\).
б) Докажите, что \(\Delta A_1B_1C_1 = \Delta A_2B_2C_2\).
Так как через две параллельные прямые \(A_1A_2\) и \(C_1C_2\) проходит плоскость \(y\), и притом только одна плоскость \(A_1A_2C_2C_1\), обозначим ее \(y\). Если две параллельные плоскости (\(x\) параллельна \(B\)) пересечены третьей (\(y\)), то линии их пересечения параллельны (\(A_1C_1\) параллельна \(A_2C_2\)). \(A_1A_2\) параллельна \(C_1C_2\), следовательно, \(A_1A_2C_2C_1\) является параллелограммом. Аналогично \(A_1B_1B_2A_2\) и \(B_1C_1C_2B_2\) также являются параллелограммами. \(A_1C_1 = A_2C_2\), \(A_1B_1 = A_2B_2\), \(B_1C_1 = B_2C_2\) (по свойству параллелограмма), следовательно, \(\triangle A_1B_1C_1 = \triangle A_2B_2C_2\) по третьему признаку равенства треугольников.
Решение:
Так как через две параллельные прямые \(A_1A_2\) и \(C_1C_2\) проходит плоскость \(y\), и притом только одна плоскость \(A_1A_2C_2C_1\), обозначим ее \(y\).
Рассмотрим плоскость \(y\):
Если две параллельные плоскости (\(x\) параллельна \(B\)) пересечены третьей (\(y\)), то линии их пересечения параллельны (\(A_1C_1\) параллельна \(A_2C_2\)).
а) Рассмотрим \(A_1A_2C_2C_1\) в плоскости \(y\):
По определению параллелограмма, \(A_1A_2\) параллельна \(C_1C_2\), следовательно, \(A_1A_2C_2C_1\) является параллелограммом. Аналогично доказывается, что \(A_1B_1B_2A_2\) и \(B_1C_1C_2B_2\) также являются параллелограммами.
б) Рассмотрим параллелограммы из пункта а):
\(A_1C_1 = A_2C_2\), \(A_1B_1 = A_2B_2\), \(B_1C_1 = B_2C_2\) (по свойству параллелограмма). Следовательно, \(\triangle A_1B_1C_1 = \triangle A_2B_2C_2\) по третьему признаку равенства треугольников. Что и требовалось доказать.
Ответ:
а) Четырехугольники \(A_1A_2B_2B_1\), \(A_1C_1C_2A_2\), \(B_1B_2C_2C_1\) являются параллелограммами.
б) Что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!