ГДЗ по Геометрии 10 класс Номер 54 Атанасян — Подробные Ответы

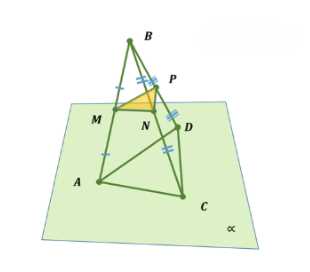
Точка \(B\) не лежит в плоскости треугольника \(ADC\), точки \(M\), \(N\) и \(P\) — середины отрезков \(BA\), \(BC\) и \(BD\) соответственно.
а) Докажите, что плоскости \(MNP\) и \(ADC\) параллельны.
б) Найдите площадь треугольника \(MNP\), если площадь треугольника \(ADC\) равна \(48\) см\(^2\).

а) Доказательство параллельности плоскостей MNP и ADC основано на теореме: «Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны». Здесь прямые AC и CD лежат в плоскости ADC, а прямые MN и NP — в плоскости MNP, при этом AC || MN и CD || NP.

б) Площадь треугольника MNP находится с использованием признака подобия треугольников: \(S_{\text{MNP}} = k^2 \cdot S_{\text{ADC}}\), где \(k = \frac{1}{2}\) — коэффициент подобия, так как MN = \(\frac{1}{2}\)AC. Подставляя \(S_{\text{ADC}} = 48 \text{ см}^2\), получаем \(S_{\text{MNP}} = \left(\frac{1}{2}\right)^2 \cdot 48 \text{ см}^2 = 12 \text{ см}^2\).

а) Для доказательства параллельности плоскостей MNP и ADC воспользуемся теоремой: «Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны».

В данном случае:
— Прямые AC и CD лежат в плоскости ADC.
— Прямые MN и NP лежат в плоскости MNP.
— Согласно условию, AC || MN и CD || NP.

Следовательно, по теореме, плоскости ADC и MNP параллельны.

б) Для нахождения площади треугольника MNP воспользуемся признаком подобия треугольников:
— Треугольники AMN и ACD подобны, так как AC || MN и AB || MN (по построению).
— Коэффициент подобия \(k = \frac{1}{2}\), так как MN = \(\frac{1}{2}\)AC.

Площадь треугольника MNP равна:
\(S_{\text{MNP}} = k^2 \cdot S_{\text{ADC}} = \left(\frac{1}{2}\right)^2 \cdot 48 \text{ см}^2 = 12 \text{ см}^2\)