
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 47 Атанасян — Подробные Ответы
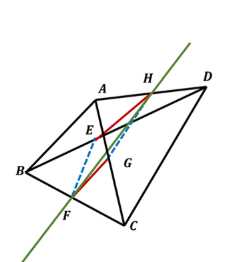
В пространственном четырёхугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны. Докажите, что прямые \(AB\) и \(CD\) образуют равные углы с прямой, проходящей через середины отрезков \(BC\) и \(AD\).
В пространственном четырёхугольнике \(ABCD\) с равными сторонами \(AB\) и \(CD\), построив дополнительные отрезки \(BE = ED\) и \(AG = GC\), получаем, что четырёхугольник \(EFGH\) является параллелограммом. Рассмотрев треугольники \(AADC\) и \(ABDC\), видим, что их средние линии \(HG\) и \(EF\) параллельны и равны половине соответствующих сторон. Следовательно, \(EH = FG = \frac{AB}{2} = \frac{CD}{2}\), и четырёхугольник \(EFGH\) является ромбом. Поскольку \(HF\) является диагональю ромба \(EFGH\), углы \(\angle LEH F\) и \(\angle LGH F\) равны, что доказывает, что прямые \(AB\) и \(CD\) образуют равные углы с прямой, проходящей через середины отрезков \(BC\) и \(AD\).
В пространственном четырёхугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны. Докажем, что прямые \(AB\) и \(CD\) образуют равные углы с прямой, проходящей через середины отрезков \(BC\) и \(AD\).
Построим дополнительные вспомогательные элементы: отрезки \(BE = ED\) и \(AG = GC\). Тогда четырёхугольник \(EFGH\) является параллелограммом. Это можно доказать, используя признак параллелограмма: если в четырёхугольнике противоположные стороны равны и параллельны, то этот четырёхугольник является параллелограммом.
Рассмотрим два треугольника \(AADC\) и \(ABDC\). По построению, средние линии \(HG\) и \(EF\) этих треугольников параллельны: \(HG \parallel CD\), \(CD \parallel EF\) и \(HG = \frac{CD}{2}, EF = \frac{CD}{2}\). Согласно свойству параллельных прямых, прямые \(HG\) и \(EF\) также параллельны: \(HG \parallel EF\).
Более того, проведя аналогичные рассуждения, можно доказать, что \(EH = FG = \frac{AB}{2} = \frac{CD}{2} = EF = HG\), то есть четырёхугольник \(EFGH\) является ромбом.
Осталось доказать равенство углов. По определению, угол между \(AB\) и \(HF\) равен \(\angle LEH F\), а угол между \(CD\) и \(HF\) равен \(\angle LGH F\). Поскольку \(HF\) является диагональю ромба \(EFGH\), то \(\angle LEH F = \angle LGH F\). Следовательно, прямые \(AB\) и \(CD\) образуют равные углы с прямой, проходящей через середины отрезков \(BC\) и \(AD\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!