
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 44 Атанасян — Подробные Ответы
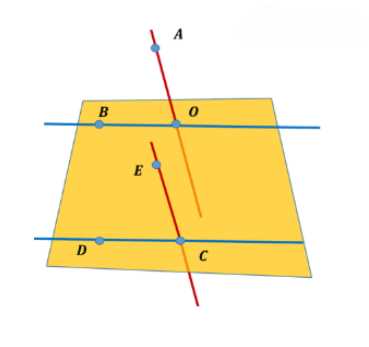
Прямые \(OB\) и \(CD\) параллельны, а \(OA\) и \(CD\) — скрещивающиеся прямые. Найдите угол между прямыми \(OA\) и \(CD\), если:
а) \(\angle AOB = 40^\circ\);
б) \(\angle AOB = 135^\circ\);
в) \(\angle AOB = 90^\circ\).
Так как прямые \(OB\) и \(CD\) параллельны, а \(OA\) и \(CD\) скрещивающиеся, то углы \(\angle AOB\) и \(\angle ECD\) являются сонаправленными, т.е. \(\angle AOB = \angle ECD\). Следовательно, а) при \(\angle AOB = 40^\circ\), \(\angle ECD = 40^\circ\); б) при \(\angle AOB = 135^\circ\), \(\angle ECD = 135^\circ\), но так как угол между прямыми не может быть больше \(90^\circ\), то \(\angle ECD = 45^\circ\); в) при \(\angle AOB = 90^\circ\), \(\angle ECD = 90^\circ\).
Для решения данной задачи необходимо использовать свойство сонаправленных углов. Так как прямые \(OB\) и \(CD\) параллельны, а прямые \(OA\) и \(CD\) скрещивающиеся, то углы \(\angle AOB\) и \(\angle ECD\) являются сонаправленными. Это означает, что \(\angle AOB = \angle ECD\).
а) Если \(\angle AOB = 40^\circ\), то \(\angle ECD = 40^\circ\). Следовательно, угол между прямыми \(OA\) и \(CD\) равен \(40^\circ\).
б) Если \(\angle AOB = 135^\circ\), то \(\angle ECD = 135^\circ\). Однако, так как угол между прямыми не может быть больше \(90^\circ\), то необходимо рассмотреть смежный угол. Таким образом, угол между прямыми \(OA\) и \(CD\) равен \(45^\circ\).
в) Если \(\angle AOB = 90^\circ\), то \(\angle ECD = 90^\circ\). Следовательно, угол между прямыми \(OA\) и \(CD\) равен \(90^\circ\).
Ответ:
а) Угол между прямыми \(OA\) и \(CD\) равен \(40^\circ\).
б) Угол между прямыми \(OA\) и \(CD\) равен \(45^\circ\).
в) Угол между прямыми \(OA\) и \(CD\) равен \(90^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!