Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 437 Атанасян — Подробные Ответы
В конус вписана сфера радиуса r. Найдите площадь полной поверхности конуса, если угол между образующей и основанием конуса равен \(\alpha\)
Решение:
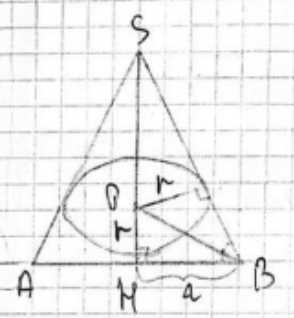
\(SH\) — высота конуса, \(OB\) — биссектриса угла \(HBS\), следовательно \(\angle OBH = \frac{\alpha}{2}\).
В треугольнике \(OBH\): \(\frac{r}{BH} = \tan\frac{\alpha}{2}\), откуда \(BH = \frac{r}{\tan\frac{\alpha}{2}}\).
Площадь основания конуса: \(S_{осн} = \pi \cdot BH^2 = \pi \left(\frac{r}{\tan\frac{\alpha}{2}}\right)^2 = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}}\).
Пусть \(SB = L\) — образующая конуса. Из треугольника \(SHB\): \(\frac{BH}{L} = \cos \alpha\), откуда \(L = \frac{BH}{\cos \alpha} = \frac{r}{\tan\frac{\alpha}{2}\cos \alpha}\).
Площадь боковой поверхности конуса: \(S_{бок} = \pi \cdot BH \cdot L = \pi \cdot \frac{r}{\tan\frac{\alpha}{2}} \cdot \frac{r}{\tan\frac{\alpha}{2}\cos \alpha} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}\cos \alpha}\).
Площадь полной поверхности конуса: \(S_{полн} = S_{осн} + S_{бок} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}} + \frac{\pi r^2}{\tan^2\frac{\alpha}{2}\cos \alpha} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}}\left(1 + \frac{1}{\cos \alpha}\right)\).
Упростим выражение в скобках: \(1 + \frac{1}{\cos \alpha} = \frac{\cos \alpha + 1}{\cos \alpha}\). Используя формулу \(1 + \cos \alpha = 2\cos^2\frac{\alpha}{2}\), получаем \(\frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha}\).
Тогда \(S_{полн} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha} = \frac{\pi r^2}{\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha} = \frac{\pi r^2 \cos^2\frac{\alpha}{2}}{\sin^2\frac{\alpha}{2}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha} = \frac{2\pi r^2 \cos^4\frac{\alpha}{2}}{\sin^2\frac{\alpha}{2}\cos \alpha}\).
Используя \(\tan^2\frac{\alpha}{2} = \frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}\), окончательно получаем \(S_{полн} = \frac{2\pi r^2 \cos^2\frac{\alpha}{2}}{\tan^2\frac{\alpha}{2}\cos \alpha}\).
Решение задачи состоит в нахождении площади полной поверхности конуса, в который вписана сфера радиуса \(r\), при известном угле \(\alpha\) между образующей конуса и его основанием.
Рассмотрим осевое сечение конуса, которое представляет собой равнобедренный треугольник \(SAB\), где \(S\) — вершина конуса, \(AB\) — диаметр основания. \(SH\) является высотой конуса, где \(H\) — центр основания. Вписанная сфера касается основания конуса в точке \(H\) и боковой поверхности по окружности. В осевом сечении сфера представлена окружностью с центром \(O\) на высоте \(SH\) и радиусом \(r\). Эта окружность касается основания \(AB\) в точке \(H\) и образующих \(SA\) и \(SB\).
Центр вписанной сферы \(O\) лежит на биссектрисе угла между образующей и основанием в осевом сечении. Рассмотрим прямоугольный треугольник \(SHB\), где \(\angle SHB = 90^\circ\), \(\angle SBH = \alpha\). Линия \(OB\) является биссектрисой угла \(\angle SBH\), поэтому \(\angle OBH = \frac{\alpha}{2}\).
Рассмотрим прямоугольный треугольник \(OBH\). В этом треугольнике \(OH\) — это радиус вписанной сферы \(r\), а \(BH\) — радиус основания конуса. Используя определение тангенса в прямоугольном треугольнике, мы можем связать \(OH\), \(BH\) и угол \(\angle OBH\):
\(\tan(\angle OBH) = \frac{OH}{BH}\)
\(\tan\frac{\alpha}{2} = \frac{r}{BH}\)
Из этого соотношения выразим радиус основания конуса \(BH\):
\(BH = \frac{r}{\tan\frac{\alpha}{2}}\)
Площадь основания конуса \(S_{осн}\) вычисляется как площадь круга с радиусом \(BH\):
\(S_{осн} = \pi \cdot BH^2 = \pi \left(\frac{r}{\tan\frac{\alpha}{2}}\right)^2 = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}}\)
Теперь найдем длину образующей конуса \(L = SB\). В прямоугольном треугольнике \(SHB\) угол \(\angle SBH = \alpha\). Используя определение косинуса, свяжем \(BH\), \(SB\) и угол \(\alpha\):
\(\cos \alpha = \frac{BH}{SB}\)
\(\cos \alpha = \frac{BH}{L}\)
Выразим \(L\) через \(BH\) и \(\cos \alpha\):
\(L = \frac{BH}{\cos \alpha}\)
Подставим ранее найденное выражение для \(BH\):
\(L = \frac{\frac{r}{\tan\frac{\alpha}{2}}}{\cos \alpha} = \frac{r}{\tan\frac{\alpha}{2}\cos \alpha}\)
Площадь боковой поверхности конуса \(S_{бок}\) вычисляется по формуле \(\pi \cdot \text{радиус основания} \cdot \text{образующая}\):
\(S_{бок} = \pi \cdot BH \cdot L\)
Подставим выражения для \(BH\) и \(L\):
\(S_{бок} = \pi \cdot \frac{r}{\tan\frac{\alpha}{2}} \cdot \frac{r}{\tan\frac{\alpha}{2}\cos \alpha} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}\cos \alpha}\)
Площадь полной поверхности конуса \(S_{полн}\) равна сумме площади основания и площади боковой поверхности:
\(S_{полн} = S_{осн} + S_{бок}\)
\(S_{полн} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}} + \frac{\pi r^2}{\tan^2\frac{\alpha}{2}\cos \alpha}\)
Вынесем общий множитель \(\frac{\pi r^2}{\tan^2\frac{\alpha}{2}}\):
\(S_{полн} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}} \left(1 + \frac{1}{\cos \alpha}\right)\)
Упростим выражение в скобках. Приведем к общему знаменателю:
\(1 + \frac{1}{\cos \alpha} = \frac{\cos \alpha}{\cos \alpha} + \frac{1}{\cos \alpha} = \frac{\cos \alpha + 1}{\cos \alpha}\)
Используем формулу двойного угла для косинуса: \(\cos \alpha = 2\cos^2\frac{\alpha}{2} — 1\), откуда \(1 + \cos \alpha = 2\cos^2\frac{\alpha}{2}\).
Тогда выражение в скобках становится:
\(\frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha}\)
Подставим это обратно в выражение для \(S_{полн}\):
\(S_{полн} = \frac{\pi r^2}{\tan^2\frac{\alpha}{2}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha}\)
Заменим \(\tan^2\frac{\alpha}{2}\) на \(\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}\):
\(S_{полн} = \frac{\pi r^2}{\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha}\)
\(S_{полн} = \frac{\pi r^2 \cos^2\frac{\alpha}{2}}{\sin^2\frac{\alpha}{2}} \cdot \frac{2\cos^2\frac{\alpha}{2}}{\cos \alpha}\)
\(S_{полн} = \frac{2\pi r^2 \cos^4\frac{\alpha}{2}}{\sin^2\frac{\alpha}{2}\cos \alpha}\)
Это выражение можно также записать, используя \(\tan^2\frac{\alpha}{2}\) в знаменателе:
\(S_{полн} = \frac{2\pi r^2 \cos^2\frac{\alpha}{2}}{\frac{\sin^2\frac{\alpha}{2}}{\cos^2\frac{\alpha}{2}}\cos \alpha} = \frac{2\pi r^2 \cos^2\frac{\alpha}{2}}{\tan^2\frac{\alpha}{2}\cos \alpha}\)
Таким образом, площадь полной поверхности конуса равна \(\frac{2\pi r^2 \cos^2\frac{\alpha}{2}}{\tan^2\frac{\alpha}{2}\cos \alpha}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.