Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 436 Атанасян — Подробные Ответы
В конус с углом \(\phi\) при вершине осевого сечения и радиусом основания r вписана сфера радиуса R (т. е. сфера касается основания конуса и каждой его образующей, рис. 129, б). Найдите: а) r, если известны R и \(\phi\); б) R, если известны r и \(\phi\); в) \(\phi\), если \(R = 1\) см, \(r = \sqrt{3}\) см.
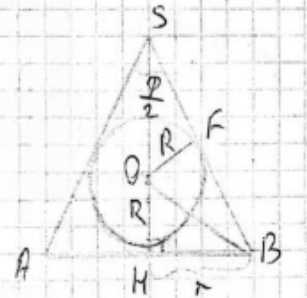
Рассмотрим осевое сечение конуса со вписанной сферой. В этом сечении мы видим равнобедренный треугольник (осевое сечение конуса) и вписанную в него окружность (осевое сечение сферы). Высота конуса делит угол при вершине \(\phi\) пополам. В прямоугольном треугольнике, образованном высотой, радиусом основания и образующей конуса, угол при основании равен \(90^\circ — \frac{\phi}{2}\). Центр вписанной сферы лежит на биссектрисе угла при основании конуса в осевом сечении. Следовательно, угол между радиусом основания конуса и отрезком, соединяющим центр сферы с точкой касания на основании, равен половине угла при основании, то есть \(\frac{90^\circ — \frac{\phi}{2}}{2} = 45^\circ — \frac{\phi}{4}\). В прямоугольном треугольнике, образованном радиусом сферы R (проведенным к точке касания на основании), радиусом основания конуса r, и отрезком, соединяющим центр сферы с центром основания конуса, тангенс этого угла равен отношению противолежащего катета (радиус сферы R) к прилежащему катету (радиус основания конуса r). Таким образом, имеем соотношение \(\frac{R}{r} = \tan(45^\circ — \frac{\phi}{4})\).
а) Чтобы найти r, если известны R и \(\phi\), выразим r из полученного соотношения: \(r = \frac{R}{\tan(45^\circ — \frac{\phi}{4})}\). Используя тригонометрическое тождество \(\frac{1}{\tan(x)} = \cot(x)\) и \(\cot(x) = \tan(90^\circ — x)\), можем также записать \(r = R \cot(45^\circ — \frac{\phi}{4}) = R \tan(90^\circ — (45^\circ — \frac{\phi}{4})) = R \tan(45^\circ + \frac{\phi}{4})\).
б) Чтобы найти R, если известны r и \(\phi\), выразим R из соотношения \(\frac{R}{r} = \tan(45^\circ — \frac{\phi}{4})\): \(R = r \tan(45^\circ — \frac{\phi}{4})\).
в) Дано \(R = 1\) см и \(r = \sqrt{3}\) см. Подставим эти значения в основное соотношение \(\frac{R}{r} = \tan(45^\circ — \frac{\phi}{4})\): \(\frac{1}{\sqrt{3}} = \tan(45^\circ — \frac{\phi}{4})\). Известно, что \(\tan(30^\circ) = \frac{1}{\sqrt{3}}\). Следовательно, \(45^\circ — \frac{\phi}{4} = 30^\circ\). Решая это уравнение относительно \(\frac{\phi}{4}\), получаем \(\frac{\phi}{4} = 45^\circ — 30^\circ = 15^\circ\). Умножая обе части на 4, находим \(\phi = 4 \times 15^\circ = 60^\circ\).
Рассмотрим осевое сечение данного конуса со вписанной сферой. В осевом сечении мы видим равнобедренный треугольник, представляющий конус, и вписанную в него окружность, представляющую сферу. Вершина треугольника соответствует вершине конуса, основание треугольника — диаметру основания конуса. Высота конуса является осью симметрии осевого сечения и делит угол при вершине конуса \(\phi\) на два равных угла по \(\frac{\phi}{2}\).
Рассмотрим один из двух прямоугольных треугольников, на которые высота делит осевое сечение. Катетами этого треугольника являются высота конуса (обозначим ее H) и радиус основания конуса (r), а гипотенузой — образующая конуса (l). Угол при вершине этого прямоугольного треугольника равен \(\frac{\phi}{2}\), а угол при основании равен \(90^\circ — \frac{\phi}{2}\).
Центр вписанной сферы лежит на высоте конуса. Поскольку сфера касается основания конуса, радиус сферы R, опущенный из центра сферы на основание, перпендикулярен основанию и равен R. Этот радиус совпадает с отрезком высоты конуса от центра сферы до основания.
Сфера также касается образующей конуса. Радиус сферы R, проведенный в точку касания на образующей, перпендикулярен образующей.
Центр вписанной окружности в треугольник (что соответствует центру вписанной сферы в конус в осевом сечении) находится на пересечении биссектрис углов треугольника. Рассмотрим угол при основании прямоугольного треугольника осевого сечения, который равен \(90^\circ — \frac{\phi}{2}\). Биссектриса этого угла проходит через центр вписанной сферы. Угол между радиусом основания конуса (который лежит на основании треугольника осевого сечения) и этой биссектрисой равен половине угла при основании, то есть \(\frac{90^\circ — \frac{\phi}{2}}{2} = 45^\circ — \frac{\phi}{4}\).
Теперь рассмотрим прямоугольный треугольник, образованный радиусом вписанной сферы R, проведенным к основанию конуса, отрезком радиуса основания конуса r от точки касания сферы с основанием до центра основания конуса, и отрезком, соединяющим центр сферы с центром основания конуса. В этом прямоугольном треугольнике один катет равен радиусу сферы R, а другой катет равен радиусу основания конуса r. Угол, противолежащий катету R, равен углу между радиусом основания конуса и биссектрисой угла при основании большого прямоугольного треугольника осевого сечения, который мы ранее нашли равным \(45^\circ — \frac{\phi}{4}\).
В этом прямоугольном треугольнике тангенс угла \(45^\circ — \frac{\phi}{4}\) равен отношению противолежащего катета к прилежащему катету. Противолежащий катет равен R, а прилежащий катет равен r. Таким образом, получаем основное соотношение: \(\tan(45^\circ — \frac{\phi}{4}) = \frac{R}{r}\).
а) Найдем r, если известны R и \(\phi\). Из основного соотношения выразим r: \(r = \frac{R}{\tan(45^\circ — \frac{\phi}{4})}\). Используя свойство котангенса \(\frac{1}{\tan(x)} = \cot(x)\), можно записать \(r = R \cot(45^\circ — \frac{\phi}{4})\). Также, используя свойство \(\cot(x) = \tan(90^\circ — x)\), получим \(r = R \tan(90^\circ — (45^\circ — \frac{\phi}{4})) = R \tan(45^\circ + \frac{\phi}{4})\).
б) Найдем R, если известны r и \(\phi\). Из основного соотношения выразим R: \(R = r \tan(45^\circ — \frac{\phi}{4})\).
в) Найдем \(\phi\), если \(R = 1\) см и \(r = \sqrt{3}\) см. Подставим данные значения в основное соотношение: \(\frac{1}{\sqrt{3}} = \tan(45^\circ — \frac{\phi}{4})\). Известно, что \(\tan(30^\circ) = \frac{1}{\sqrt{3}}\). Следовательно, \(45^\circ — \frac{\phi}{4} = 30^\circ\). Решим это уравнение относительно \(\frac{\phi}{4}\): \(\frac{\phi}{4} = 45^\circ — 30^\circ = 15^\circ\). Умножим обе части на 4, чтобы найти \(\phi\): \(\phi = 4 \times 15^\circ = 60^\circ\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.