ГДЗ по Геометрии 10 класс Номер 435 Атанасян — Подробные Ответы

Сфера вписана в цилиндр (т. е. она касается оснований цилиндра и каждой его образующей, рис. 129, а). Найдите отношение площади сферы к площади полной поверхности цилиндра

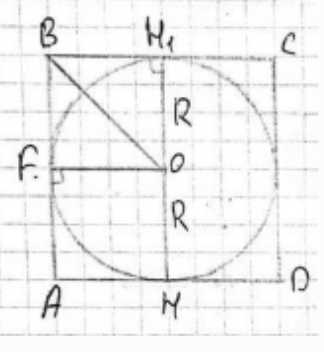
Рассмотрим осевое сечение. \(R\) — радиус сферы. \(ABCD\) — квадрат. \(BH_1 = OH_1 = R\). \(BH_1\) — радиус основания цилиндра, \(HH_1 = 2R\) — высота цилиндра.

Площадь полной поверхности цилиндра \(S_{\text{полн}} = S_{\text{бок}} + 2S_{\text{осн}}\). Площадь боковой поверхности цилиндра \(S_{\text{бок}} = 2 \pi \cdot BH_1 \cdot HH_1 = 2 \pi R \cdot 2R = 4 \pi R^2\). Площадь основания цилиндра \(S_{\text{осн}} = \pi \cdot BH_1^2 = \pi R^2\). Площадь полной поверхности цилиндра \(S_{\text{полн}} = 4 \pi R^2 + 2 \pi R^2 = 6 \pi R^2\). Площадь поверхности сферы \(S_{\text{сферы}} = 4 \pi R^2\). Отношение площади сферы к площади полной поверхности цилиндра равно \(\frac{S_{\text{сферы}}}{S_{\text{полн}}} = \frac{4 \pi R^2}{6 \pi R^2} = \frac{2}{3}\).

Рассмотрим осевое сечение данной конфигурации, состоящей из сферы, вписанной в цилиндр. В осевом сечении мы увидим окружность (сечение сферы) вписанную в прямоугольник (сечение цилиндра). Поскольку сфера касается оснований цилиндра и его боковой поверхности, этот прямоугольник является квадратом. Обозначим радиус сферы как \(R\). Из условия вписанности следует, что радиус основания цилиндра также равен радиусу сферы, то есть \(r_{\text{цил}} = R\). Высота цилиндра в этом случае будет равна диаметру сферы, то есть \(h_{\text{цил}} = 2R\).

Теперь вычислим площади поверхностей. Площадь поверхности сферы определяется формулой \(S_{\text{сферы}} = 4 \pi R^2\).

Площадь полной поверхности цилиндра состоит из площади боковой поверхности и площадей двух оснований. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. Длина окружности основания равна \(2 \pi r_{\text{цил}}\), а высота цилиндра \(h_{\text{цил}}\). Подставляя наши значения, получаем \(S_{\text{бок}} = 2 \pi R \cdot 2R = 4 \pi R^2\).

Площадь основания цилиндра равна площади круга с радиусом \(r_{\text{цил}}\). \(S_{\text{осн}} = \pi r_{\text{цил}}^2 = \pi R^2\). Поскольку у цилиндра два основания, их общая площадь равна \(2S_{\text{осн}} = 2 \pi R^2\).

Полная площадь поверхности цилиндра \(S_{\text{полн}}\) равна сумме площади боковой поверхности и площадей двух оснований: \(S_{\text{полн}} = S_{\text{бок}} + 2S_{\text{осн}} = 4 \pi R^2 + 2 \pi R^2 = 6 \pi R^2\).

Наконец, найдем отношение площади сферы к площади полной поверхности цилиндра: \(\frac{S_{\text{сферы}}}{S_{\text{полн}}} = \frac{4 \pi R^2}{6 \pi R^2}\). Сокращая \(\pi R^2\) в числителе и знаменателе, получаем \(\frac{4}{6}\), что упрощается до \(\frac{2}{3}\). Таким образом, отношение площади сферы к площади полной поверхности цилиндра составляет \(\frac{2}{3}\).