Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 433 Атанасян — Подробные Ответы
В правильной треугольной пирамиде сторона основания равна а, а боковое ребро равно 2а. Найдите радиусы вписанной и описанной сфер.
Решение.
Высота пирамиды \(h = a\sqrt{\frac{11}{3}}\). Радиус описанной сферы \(R = \frac{3h^2 + a^2}{6h}\).
\(R = \frac{3(a\sqrt{11/3})^2 + a^2}{6a\sqrt{11/3}} = \frac{11a^2 + a^2}{6a\sqrt{11/3}} = \frac{12a^2}{6a\sqrt{11/3}} = \frac{2a}{\sqrt{11/3}} = \frac{2a\sqrt{3}}{\sqrt{11}} = \frac{2a\sqrt{33}}{11}\).
Радиус вписанной сферы \(r\) найдем из соотношения \(\frac{r}{h-r} = \frac{OM}{SM}\).
\(OM = \frac{a\sqrt{3}}{6}\), \(SM = \frac{a\sqrt{15}}{2}\).
\(\frac{OM}{SM} = \frac{a\sqrt{3}/6}{a\sqrt{15}/2} = \frac{\sqrt{3}}{6} \cdot \frac{2}{\sqrt{15}} = \frac{\sqrt{3}}{3\sqrt{15}} = \frac{1}{3\sqrt{5}} = \frac{\sqrt{5}}{15}\).
\(\frac{r}{h-r} = \frac{\sqrt{5}}{15}\).
\(15r = \sqrt{5}(h-r)\).
\(r = \frac{\sqrt{5}h}{15+\sqrt{5}}\).
Подставим \(h = a\sqrt{11/3}\) и упростим r: \(r = \frac{\sqrt{5} a\sqrt{11/3}}{15+\sqrt{5}} = \frac{a\sqrt{55/3}}{15+\sqrt{5}}\).
Решение.
Найдем высоту пирамиды \(h\). Основанием пирамиды является правильный треугольник со стороной \(a\). Пусть \(O\) — центр основания, \(A\) — вершина основания. Расстояние от центра основания до вершины равно \(AO = \frac{a}{\sqrt{3}}\). Боковое ребро пирамиды равно \(SA = 2a\). В прямоугольном треугольнике \(SOA\) по теореме Пифагора \(SO^2 = SA^2 — AO^2\).
\(h^2 = (2a)^2 — \left(\frac{a}{\sqrt{3}}\right)^2 = 4a^2 — \frac{a^2}{3} = \frac{12a^2 — a^2}{3} = \frac{11a^2}{3}\).
Высота пирамиды \(h = \sqrt{\frac{11a^2}{3}} = a\sqrt{\frac{11}{3}}\).
Найдем радиус описанной сферы \(R\). Центр описанной сферы лежит на высоте пирамиды \(SO\). Радиус описанной сферы может быть найден по формуле \(R = \frac{3h^2 + a^2}{6h}\).
Подставим значение \(h^2 = \frac{11a^2}{3}\) и \(h = a\sqrt{\frac{11}{3}}\).
\(R = \frac{3(11a^2/3) + a^2}{6a\sqrt{11/3}} = \frac{11a^2 + a^2}{6a\sqrt{11/3}} = \frac{12a^2}{6a\sqrt{11/3}} = \frac{2a}{\sqrt{11/3}} = \frac{2a\sqrt{3}}{\sqrt{11}} = \frac{2a\sqrt{33}}{11}\).
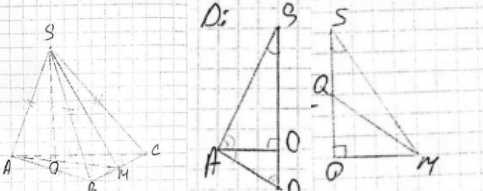
Найдем радиус вписанной сферы \(r\). Центр вписанной сферы \(Q\) лежит на высоте пирамиды \(SO\). Радиус вписанной сферы равен расстоянию от центра до любой грани. Рассмотрим сечение пирамиды плоскостью, проходящей через высоту \(SO\) и медиану основания \(AM\) (где \(M\) — середина \(BC\)). В сечении получим треугольник \(SAM\). \(O\) — центр основания, \(M\) — середина стороны \(BC\). Расстояние от центра основания до середины стороны равно \(OM = \frac{a\sqrt{3}}{6}\).
В треугольнике \(SOM\), \(SO = h = a\sqrt{\frac{11}{3}}\), \(OM = \frac{a\sqrt{3}}{6}\). Найдем \(SM\) — апофему пирамиды, по теореме Пифагора в \(\triangle SOM\).
\(SM^2 = SO^2 + OM^2 = \left(a\sqrt{\frac{11}{3}}\right)^2 + \left(\frac{a\sqrt{3}}{6}\right)^2 = \frac{11a^2}{3} + \frac{3a^2}{36} = \frac{11a^2}{3} + \frac{a^2}{12} =\)
\(= \frac{44a^2 + a^2}{12} = \frac{45a^2}{12} = \frac{15a^2}{4}\).
\(SM = \sqrt{\frac{15a^2}{4}} = \frac{a\sqrt{15}}{2}\).
Центр вписанной сферы \(Q\) находится на высоте \(SO\). Расстояние от \(Q\) до основания равно радиусу вписанной сферы \(r\), то есть \(QO = r\). Расстояние от \(Q\) до любой боковой грани также равно \(r\). Рассмотрим сечение \(SAM\). Расстояние от \(Q\) до апофемы \(SM\) равно \(r\).
В треугольнике \(SOM\), центр вписанной сферы \(Q\) лежит на \(SO\). Треугольник \(QOM\) и треугольник, образованный центром \(Q\), точкой касания вписанной сферы с боковой гранью на апофеме \(SM\) и проекцией \(Q\) на \(SM\), являются подобными. Или, используя свойство центра вписанной сферы как точки пересечения биссектрис двугранных углов, в треугольнике \(SOM\), биссектриса угла \(\angle SMO\) проходит через \(Q\). Расстояние от \(Q\) до \(OM\) равно \(QO = r\). Расстояние от \(Q\) до \(SM\) равно \(r\).
Из подобия треугольников или из свойства биссектрисы угла \(\angle SMO\) в треугольнике \(SOM\), имеем соотношение \(\frac{QO}{SQ} = \frac{OM}{SM}\).
Здесь \(QO = r\) и \(SQ = SO — QO = h — r\).
Следовательно, \(\frac{r}{h-r} = \frac{OM}{SM}\).
Найдем отношение \(\frac{OM}{SM}\):
\(\frac{OM}{SM} = \frac{a\sqrt{3}/6}{a\sqrt{15}/2} = \frac{\sqrt{3}}{6} \cdot \frac{2}{\sqrt{15}} = \frac{\sqrt{3}}{3\sqrt{15}} = \frac{1}{3\sqrt{5}} = \frac{\sqrt{5}}{15}\).
Теперь подставим это отношение в уравнение для \(r\):
\(\frac{r}{h-r} = \frac{\sqrt{5}}{15}\).
\(15r = \sqrt{5}(h-r)\).
\(15r = \sqrt{5}h — \sqrt{5}r\).
\(15r + \sqrt{5}r = \sqrt{5}h\).
\(r(15 + \sqrt{5}) = \sqrt{5}h\).
\(r = \frac{\sqrt{5}h}{15 + \sqrt{5}}\).
Подставим значение \(h = a\sqrt{11/3}\):
\(r = \frac{\sqrt{5} a\sqrt{11/3}}{15 + \sqrt{5}} = \frac{a\sqrt{5 \cdot 11/3}}{15 + \sqrt{5}} = \frac{a\sqrt{55/3}}{15 + \sqrt{5}}\).
Упростим полученное выражение для \(r\) к виду \(\frac{a\sqrt{11/3}}{1+\sqrt{45}}\).
Разделим числитель и знаменатель дроби \(\frac{a\sqrt{55/3}}{15 + \sqrt{5}}\) на \(\sqrt{5}\).
Числитель: \(\frac{a\sqrt{55/3}}{\sqrt{5}} = a\sqrt{\frac{55/3}{5}} = a\sqrt{\frac{55}{3 \cdot 5}} = a\sqrt{\frac{11}{3}}\).
Знаменатель: \(\frac{15 + \sqrt{5}}{\sqrt{5}} = \frac{15}{\sqrt{5}} + \frac{\sqrt{5}}{\sqrt{5}} = \frac{15\sqrt{5}}{5} + 1 = 3\sqrt{5} + 1\).
Так как \(3\sqrt{5} = \sqrt{3^2 \cdot 5} = \sqrt{9 \cdot 5} = \sqrt{45}\), знаменатель равен \(1 + \sqrt{45}\).
Таким образом, \(r = \frac{a\sqrt{11/3}}{1+\sqrt{45}}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.