
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 432 Атанасян — Подробные Ответы
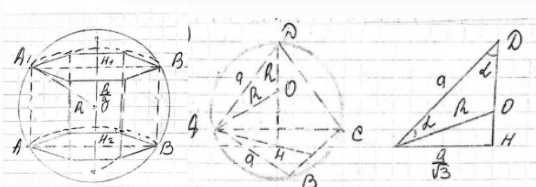
Радиус сферы равен R. Найдите площадь полной поверхности: а) вписанного в сферу куба; б) вписанной правильной шестиугольной призмы, высота которой равна R; в) вписанного правильного тетраэдра.
а) Для вписанного куба диагональ куба равна диаметру сферы \(2R\). Если ребро куба равно \(a\), то диагональ куба равна \(a\sqrt{3}\). Таким образом, \(a\sqrt{3} = 2R\), откуда \(a = \frac{2R}{\sqrt{3}}\). Площадь полной поверхности куба равна \(6a^2 = 6 \left(\frac{2R}{\sqrt{3}}\right)^2 = 6 \cdot \frac{4R^2}{3} = 8R^2\). Ответ: \(8R^2\).
б) Для вписанной правильной шестиугольной призмы высотой \(R\). Радиус описанной окружности основания призмы равен \(r\). Диаметр сферы \(2R\) является диагональю прямоугольника, образованного высотой призмы и диаметром описанной окружности основания. Следовательно, \((2r)^2 + R^2 = (2R)^2\), откуда \(4r^2 + R^2 = 4R^2\), \(4r^2 = 3R^2\), \(r = \frac{\sqrt{3}R}{2}\). Для правильного шестиугольника сторона основания \(a\) равна радиусу описанной окружности, т.е. \(a = r = \frac{\sqrt{3}R}{2}\). Площадь боковой поверхности призмы равна \(6 \cdot a \cdot R = 6 \cdot \frac{\sqrt{3}R}{2} \cdot R = 3\sqrt{3}R^2\). Площадь основания правильного шестиугольника равна \(\frac{3\sqrt{3}}{2} a^2 = \frac{3\sqrt{3}}{2} \left(\frac{\sqrt{3}R}{2}\right)^2 = \frac{3\sqrt{3}}{2} \cdot \frac{3R^2}{4} = \frac{9\sqrt{3}R^2}{8}\). Площадь полной поверхности призмы равна \(2 \cdot S_{осн} + S_{бок} = 2 \cdot \frac{9\sqrt{3}R^2}{8} + 3\sqrt{3}R^2 = \frac{9\sqrt{3}R^2}{4} + \frac{12\sqrt{3}R^2}{4} = \frac{21\sqrt{3}R^2}{4}\). Ответ: \(\frac{21\sqrt{3}}{4}R^2\).
в) Для вписанного правильного тетраэдра с ребром \(a\). Радиус описанной сферы \(R\) связан с ребром тетраэдра соотношением \(R = \frac{a\sqrt{6}}{4}\), откуда \(a = \frac{4R}{\sqrt{6}} = \frac{2R\sqrt{6}}{3}\). Площадь одной грани тетраэдра (правильного треугольника) равна \(\frac{a^2\sqrt{3}}{4}\). Площадь полной поверхности тетраэдра равна \(4 \cdot \frac{a^2\sqrt{3}}{4} = a^2\sqrt{3}\). Подставляя значение \(a\), получим \(\left(\frac{2R\sqrt{6}}{3}\right)^2 \sqrt{3} = \frac{4R^2 \cdot 6}{9} \sqrt{3} = \frac{24R^2}{9} \sqrt{3} = \frac{8R^2}{3} \sqrt{3} = \frac{8\sqrt{3}}{3}R^2\). Ответ: \(\frac{8\sqrt{3}}{3}R^2\).
Радиус сферы равен \(R\). Требуется найти площадь полной поверхности трех тел, вписанных в эту сферу.
а) Найдем площадь полной поверхности куба, вписанного в сферу радиуса \(R\).
Когда куб вписан в сферу, все его вершины лежат на поверхности сферы. Диагональ куба, соединяющая две наиболее удаленные вершины, проходит через центр сферы и равна диаметру сферы. Диаметр сферы равен \(2R\).
Пусть ребро куба равно \(a\). Диагональ грани куба равна \(a\sqrt{2}\). Диагональ куба \(d\) может быть найдена по теореме Пифагора в прямоугольном треугольнике, образованном ребром куба, диагональю грани и диагональю куба: \(d^2 = a^2 + (a\sqrt{2})^2 = a^2 + 2a^2 = 3a^2\), следовательно, \(d = a\sqrt{3}\).
Приравнивая диагональ куба к диаметру сферы, получаем уравнение \(a\sqrt{3} = 2R\).
Выразим ребро куба \(a\) через радиус сферы \(R\): \(a = \frac{2R}{\sqrt{3}}\).
Полная поверхность куба состоит из шести равных квадратных граней. Площадь одной грани равна \(a^2\).
Площадь полной поверхности куба \(S_{куба} = 6a^2\).
Подставим найденное значение \(a\): \(S_{куба} = 6 \left(\frac{2R}{\sqrt{3}}\right)^2 = 6 \cdot \frac{(2R)^2}{(\sqrt{3})^2} = 6 \cdot \frac{4R^2}{3} = \frac{24R^2}{3} = 8R^2\).
Таким образом, площадь полной поверхности куба, вписанного в сферу радиуса \(R\), равна \(8R^2\).
б) Найдем площадь полной поверхности правильной шестиугольной призмы, вписанной в сферу радиуса \(R\), если высота призмы равна \(R\).
Правильная шестиугольная призма вписана в сферу, это означает, что все вершины обоих оснований призмы лежат на поверхности сферы. Высота призмы задана и равна \(R\).
Рассмотрим сечение сферы и призмы плоскостью, проходящей через ось призмы и две противоположные вершины на каждом из оснований. В этом сечении получится прямоугольник, вписанный в большое круговое сечение сферы. Диагональ этого прямоугольника является диаметром сферы, равным \(2R\).
Пусть сторона правильного шестиугольника в основании призмы равна \(a\). Расстояние между противоположными вершинами правильного шестиугольника равно \(2a\), и это является диаметром окружности, описанной вокруг основания.
В прямоугольном сечении призмы стороны равны высоте призмы \(R\) и диаметру описанной окружности основания \(2a\). По теореме Пифагора для диагонали этого прямоугольника имеем: \((2a)^2 + R^2 = (2R)^2\).
Решим это уравнение относительно \(a\): \(4a^2 + R^2 = 4R^2\), \(4a^2 = 3R^2\), \(a^2 = \frac{3R^2}{4}\), откуда \(a = \sqrt{\frac{3R^2}{4}} = \frac{\sqrt{3}R}{2}\).
Полная поверхность призмы состоит из двух площадей оснований и площади боковой поверхности.
Основанием является правильный шестиугольник со стороной \(a\). Площадь правильного шестиугольника может быть найдена как сумма площадей шести правильных треугольников со стороной \(a\). Площадь правильного треугольника со стороной \(a\) равна \(\frac{a^2\sqrt{3}}{4}\).
Площадь одного основания \(S_{осн} = 6 \cdot \frac{a^2\sqrt{3}}{4} = \frac{3a^2\sqrt{3}}{2}\).
Подставим значение \(a^2 = \frac{3R^2}{4}\): \(S_{осн} = \frac{3\sqrt{3}}{2} \cdot \frac{3R^2}{4} = \frac{9\sqrt{3}R^2}{8}\).
Площадь двух оснований равна \(2 \cdot S_{осн} = 2 \cdot \frac{9\sqrt{3}R^2}{8} = \frac{9\sqrt{3}R^2}{4}\).
Боковая поверхность призмы состоит из шести равных прямоугольников со сторонами \(a\) и \(R\) (высота призмы). Площадь одного такого прямоугольника равна \(a \cdot R\).
Площадь боковой поверхности \(S_{бок} = 6 \cdot (a \cdot R) = 6 \cdot \left(\frac{\sqrt{3}R}{2} \cdot R\right) = 6 \cdot \frac{\sqrt{3}R^2}{2} = 3\sqrt{3}R^2\).
Полная площадь поверхности призмы \(S_{призмы} = 2 \cdot S_{осн} + S_{бок} = \frac{9\sqrt{3}R^2}{4} + 3\sqrt{3}R^2\).
Чтобы сложить эти слагаемые, приведем \(3\sqrt{3}R^2\) к общему знаменателю 4: \(3\sqrt{3}R^2 = \frac{12\sqrt{3}R^2}{4}\).
Тогда \(S_{призмы} = \frac{9\sqrt{3}R^2}{4} + \frac{12\sqrt{3}R^2}{4} = \frac{(9\sqrt{3} + 12\sqrt{3})R^2}{4} = \frac{21\sqrt{3}R^2}{4}\).
Таким образом, площадь полной поверхности правильной шестиугольной призмы, вписанной в сферу радиуса \(R\) с высотой \(R\), равна \(\frac{21\sqrt{3}}{4}R^2\).
в) Найдем площадь полной поверхности правильного тетраэдра, вписанного в сферу радиуса \(R\).
Правильный тетраэдр — это многогранник с четырьмя гранями, каждая из которых является правильным (равносторонним) треугольником. Все ребра тетраэдра равны. Когда тетраэдр вписан в сферу, все его вершины лежат на поверхности сферы.
Пусть ребро правильного тетраэдра равно \(a\). Существует формула, связывающая радиус описанной сферы \(R\) правильного тетраэдра с его ребром \(a\): \(R = \frac{a\sqrt{6}}{4}\).
Выразим ребро тетраэдра \(a\) через радиус сферы \(R\): \(a\sqrt{6} = 4R\), откуда \(a = \frac{4R}{\sqrt{6}}\). Умножим числитель и знаменатель на \(\sqrt{6}\) для избавления от иррациональности в знаменателе: \(a = \frac{4R\sqrt{6}}{6} = \frac{2R\sqrt{6}}{3}\).
Полная поверхность тетраэдра состоит из четырех равных правильных треугольных граней. Площадь правильного треугольника со стороной \(a\) равна \(\frac{a^2\sqrt{3}}{4}\).
Площадь полной поверхности тетраэдра \(S_{тетраэдра} = 4 \cdot \frac{a^2\sqrt{3}}{4} = a^2\sqrt{3}\).
Подставим найденное значение \(a\): \(S_{тетраэдра} = \left(\frac{2R\sqrt{6}}{3}\right)^2 \sqrt{3} = \frac{(2R)^2 (\sqrt{6})^2}{3^2} \sqrt{3} = \frac{4R^2 \cdot 6}{9} \sqrt{3} = \frac{24R^2}{9} \sqrt{3}\).
Сократим дробь \(\frac{24}{9}\) на 3: \(\frac{24}{9} = \frac{8}{3}\).
Тогда \(S_{тетраэдра} = \frac{8R^2}{3} \sqrt{3} = \frac{8\sqrt{3}}{3}R^2\).
Таким образом, площадь полной поверхности правильного тетраэдра, вписанного в сферу радиуса \(R\), равна \(\frac{8\sqrt{3}}{3}R^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!