
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 431 Атанасян — Подробные Ответы
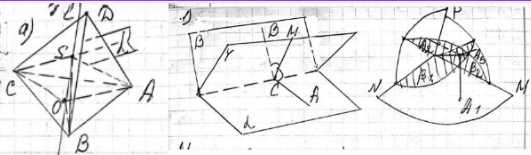
Докажите, что: а) около любого тетраэдра можно описать сферу; б) в любой тетраэдр можно вписать сферу.
Около любого тетраэдра можно описать сферу, потому что геометрическое место точек, равноудаленных от концов отрезка, есть плоскость, перпендикулярная этому отрезку и проходящая через его середину. Центр сферы, описанной около тетраэдра, должен принадлежать каждой из плоскостей, проведенных через середины ребер тетраэдра перпендикулярно этим ребрам. Если точка \(S\) равноудалена от вершин \(A, B, C\), то \(SA=SB=SC\). Расстояние от центра \(S\) до одной из вершин тетраэдра является радиусом \(R\). Сфера с центром \(S\) и радиусом \(R\) проходит через все вершины тетраэдра, и такая сфера единственна. В любой тетраэдр можно вписать сферу, потому что геометрическое место точек, равноудаленных от обеих граней двугранного угла, является биссекторной плоскостью этого двугранного угла. Центр сферы, вписанной в тетраэдр, равноудален от всех граней и принадлежит каждой из биссекторных плоскостей всех двугранных углов тетраэдра. Биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке, которая является центром вписанной сферы. Сфера с центром в этой точке и радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней, и такая сфера единственна.
В основаниях данной призмы расположены равные равносторонние треугольники. Обозначим центры этих оснований как \(A\) и \(B\). Рассмотрим верхнее основание, представленное треугольником \(PQR\). Множество всех точек, которые равноудалены от вершин \(P\), \(Q\), и \(R\) этого треугольника, представляет собой прямую, перпендикулярную плоскости треугольника \(PQR\) и проходящую через его центр \(B\). Аналогично, для нижнего основания, треугольника \(P_1Q_1R_1\), все точки, равноудаленные от его вершин \(P_1\), \(Q_1\), и \(R_1\), лежат на прямой, перпендикулярной плоскости треугольника \(P_1Q_1R_1\) и проходящей через его центр \(A\). Поскольку призма является правильной, основания \(P_1Q_1R_1\) и \(PQR\) расположены так, что их центры \(A\) и \(B\) находятся на одной вертикали, и отрезок \(AB\) перпендикулярен плоскостям обоих оснований. Следовательно, прямая, содержащая отрезок \(AB\), является геометрическим местом точек, каждая из которых равноудалена от всех вершин треугольника \(P_1Q_1R_1\) и одновременно равноудалена от всех вершин треугольника \(PQR\). Таким образом, любая точка на отрезке \(AB\) находится на одинаковом расстоянии от вершин каждого из оснований. Середина этого отрезка \(AB\), которую мы назовем точкой \(O\), обладает свойством равноудаленности от всех вершин нижнего основания \(\triangle P_1Q_1R_1\) и от всех вершин верхнего основания \(\triangle PQR\). Расстояние от точки \(O\) до любой из этих вершин одинаково и равно радиусу \(R\) сферы, которая может быть описана вокруг данной призмы. Это означает, что сфера с центром в точке \(O\) и радиусом \(R\) проходит через все вершины призмы.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!