Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 430 Атанасян — Подробные Ответы
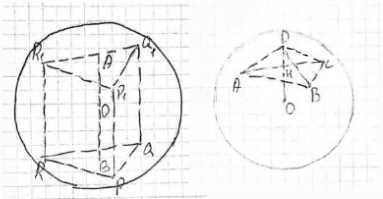
Докажите, что центр сферы, описанной около: а) правильной призмы, лежит в середине отрезка, соединяющего центры оснований этой призмы; б) правильной пирамиды, лежит на высоте этой пирамиды или её продолжении.
а) В основаниях призмы лежат равные равносторонние треугольники. Пусть \(A\) и \(B\) будут центрами оснований. Все точки, лежащие на перпендикуляре к верхнему основанию призмы, проведенном через точку \(B\), равноудалены от вершин треугольника \(PQR\). Все точки, лежащие на перпендикуляре к нижнему основанию призмы, проведенному через точку \(B\), равноудалены от вершин \(P_1Q_1R_1\). Так как призма правильная, то \(\triangle P_1Q_1R_1\) и \(\triangle PQR\) проектируются один на другой, поэтому точка \(B\) проектируется в точку \(A\) и обратно. Значит, \(AB\) перпендикулярен плоскости \(PQR\). Тогда отрезок \(AB\) есть геометрическое место точек, равноудаленных от вершин каждого из треугольников. Середина его — точка \(O\) — равноудалена от вершин \(\triangle P_1Q_1R_1\) и от вершин \(\triangle PQR\) на одинаковое расстояние \(R\), равное радиусу описанной около призмы сферы.
б) Проведем из вершины \(D\) пирамиды высоту \(DH\); \(DH\) перпендикулярен плоскости \(ABC\). Проведем отрезки \(HA\), \(HB\), \(HC\). \(\triangle DHA = \triangle DHB = \triangle DHC\) (они прямоугольные, \(DH\) — общий катет, \(AD = BD = CD\) по условию). Значит, \(HA = HB = HC = r\), где \(r\) — радиус описанной около \(\triangle ABC\) окружности. Из точки \(O\) (центр сферы) проведем отрезок \(OG\), перпендикулярный плоскости \(ABC\) (точка \(G\) на рисунке не показана). Проведем отрезки \(GA\), \(GB\), \(GC\), \(OA\), \(OB\), \(OC\). \(\triangle OGA = \triangle OGB = \triangle OGC\) (катет \(OG\) общий, \(OA = OB = OC = R\), \(R\) — радиус сферы). Значит, \(GA = GB = GC = r\), где \(r\) — радиус окружности, описанной около \(\triangle ABC\). Вокруг \(\triangle ABC\) можно описать единственную окружность, т.е. окружность имеет единственный центр и радиус. Вывод: точка \(H\) и точка \(G\) совпадают, точки \(D\), \(H\), \(O\) лежат на одной прямой. Значит, центр сферы \(O\) лежит на высоте пирамиды \(DH\) или на продолжении за точку \(H\), что и на рисунке.
а) В основаниях правильной призмы лежат равные равносторонние треугольники. Пусть \(A\) и \(B\) будут центрами оснований нижнего и верхнего соответственно. Все точки, лежащие на прямой, перпендикулярной верхнему основанию призмы и проходящей через его центр \(B\), равноудалены от вершин этого основания, то есть от вершин треугольника \(PQR\). Аналогично, все точки, лежащие на прямой, перпендикулярной нижнему основанию призмы и проходящей через его центр \(A\), равноудалены от вершин этого основания, то есть от вершин треугольника \(P_1Q_1R_1\). Поскольку призма является правильной, основания \(\triangle P_1Q_1R_1\) и \(\triangle PQR\) расположены так, что центр нижнего основания \(A\) является проекцией центра верхнего основания \(B\) на плоскость нижнего основания, и наоборот. Это означает, что отрезок \(AB\), соединяющий центры оснований, перпендикулярен плоскостям обоих оснований, например, плоскости \(PQR\). Геометрическое место точек, равноудаленных от всех вершин правильной призмы, представляет собой прямую, перпендикулярную основаниям и проходящую через их центры. Таким образом, отрезок \(AB\) является частью этой прямой. Центр сферы, описанной около призмы, должен быть равноудален от всех вершин призмы. Следовательно, он должен лежать на прямой \(AB\). Также центр сферы должен быть равноудален от вершин верхнего основания и от вершин нижнего основания. Поскольку расстояния от центра сферы до вершин верхнего основания равны, и расстояния до вершин нижнего основания равны, а также в силу симметрии правильной призмы, центр сферы будет находиться на равном расстоянии от плоскостей оснований. Единственная точка на отрезке \(AB\), равноудаленная от плоскостей оснований, это середина отрезка \(AB\). Пусть \(O\) — середина отрезка \(AB\). Тогда точка \(O\) равноудалена от вершин \(\triangle P_1Q_1R_1\) и от вершин \(\triangle PQR\) на одинаковое расстояние \(R\), которое является радиусом описанной около призмы сферы.
б) Рассмотрим правильную пирамиду с вершиной \(D\) и основанием \(\triangle ABC\). Проведем высоту пирамиды \(DH\), где \(H\) — центр основания \(\triangle ABC\). Высота \(DH\) перпендикулярна плоскости основания \(ABC\). Соединим точку \(H\) с вершинами основания отрезками \(HA\), \(HB\), \(HC\). Треугольники \(DHA\), \(DHB\), \(DHC\) являются прямоугольными, так как \(DH\) перпендикулярна плоскости \(ABC\). У этих треугольников катет \(DH\) общий. По условию пирамида правильная, что означает, что боковые ребра равны: \(AD = BD = CD\). Следовательно, по признаку равенства прямоугольных треугольников по катету и гипотенузе, \(\triangle DHA = \triangle DHB = \triangle DHC\). Из равенства этих треугольников следует равенство соответствующих катетов: \(HA = HB = HC\). Это означает, что точка \(H\) равноудалена от вершин основания \(A\), \(B\), \(C\), и следовательно, \(H\) является центром окружности, описанной около \(\triangle ABC\). Радиус этой окружности равен \(r = HA = HB = HC\). Теперь рассмотрим центр \(O\) сферы, описанной около пирамиды. Центр сферы равноудален от всех вершин пирамиды, то есть \(OA = OB = OC = OD = R\), где \(R\) — радиус сферы. Проведем из точки \(O\) перпендикуляр \(OG\) к плоскости основания \(ABC\). Точка \(G\) является проекцией центра сферы \(O\) на плоскость основания. Соединим точку \(G\) с вершинами основания отрезками \(GA\), \(GB\), \(GC\). Треугольники \(OGA\), \(OGB\), \(OGC\) являются прямоугольными с общим катетом \(OG\). Гипотенузы этих треугольников равны как радиусы описанной сферы: \(OA = OB = OC = R\). По признаку равенства прямоугольных треугольников по катету и гипотенузе, \(\triangle OGA = \triangle OGB = \triangle OGC\). Из равенства этих треугольников следует равенство соответствующих катетов: \(GA = GB = GC\). Это означает, что точка \(G\) равноудалена от вершин основания \(A\), \(B\), \(C\), и следовательно, \(G\) является центром окружности, описанной около \(\triangle ABC\). Поскольку вокруг треугольника можно описать единственную окружность с единственным центром и радиусом, центры \(H\) и \(G\) должны совпадать. Таким образом, точка \(O\) (центр сферы) лежит на прямой, перпендикулярной плоскости основания \(ABC\) и проходящей через центр описанной около основания окружности \(H\). Эта прямая совпадает с высотой пирамиды \(DH\). Следовательно, центр сферы \(O\) лежит на высоте пирамиды \(DH\) или на ее продолжении.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.