Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 43 Атанасян — Подробные Ответы
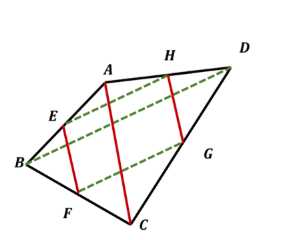
Докажите, что середины сторон пространственного четырёхугольника являются вершинами параллелограмма.
Дано: четырехугольник ABCD является пространственным, AE = EB, BF = FC, CG = GD, DH = HA. Требуется доказать, что середины сторон EFGH образуют параллелограмм.
Доказательство: Рассмотрим треугольники ΔADC и ΔBAC. Согласно теореме о средней линии треугольника, \(HG = \frac{AC}{2}\) и \(EF = \frac{AC}{2}\), следовательно, HG = EF. Аналогично можно показать, что EH = FG, то есть противоположные стороны четырехугольника EFGH равны. Кроме того, HG || AC и EF || AC, значит, HG || EF и EH || FG, то есть противоположные стороны параллельны. Таким образом, EFGH является параллелограммом.
Чтобы доказать, что середины сторон пространственного четырехугольника ABCD являются вершинами параллелограмма EFGH, необходимо показать, что противоположные стороны параллелограмма EFGH равны и параллельны.
Дано:
— Четырехугольник ABCD является пространственным.
— AE = EB, BF = FC, CG = GD, DH = HA.
Рассмотрим два треугольника: ΔADC и ΔBAC. По построению, средние линии HG и EF этих треугольников являются параллельными. Согласно теореме о средней линии треугольника, средняя линия равна половине основания, то есть \(HG = \frac{AC}{2}\) и \(EF = \frac{AC}{2}\). Следовательно, \(HG = EF\).
Аналогично, можно показать, что \(EF = HG\) и \(EH = FG\). Таким образом, противоположные стороны четырехугольника EFGH равны.
Чтобы доказать, что противоположные стороны параллельны, рассмотрим две пары параллельных прямых: HG || AC и EF || AC. Согласно свойству параллельных прямых, если две прямые параллельны третьей, то они параллельны между собой. Следовательно, HG || EF и EH || FG.
Таким образом, мы доказали, что противоположные стороны четырехугольника EFGH равны и параллельны, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.