Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 429 Атанасян — Подробные Ответы
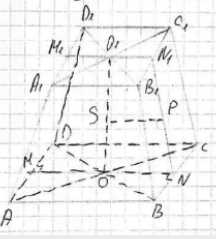
Докажите, что если в правильную усечённую четырёхугольную пирамиду можно вписать сферу, то апофема пирамиды равна полусумме сторон оснований её боковой грани.
По условию, в правильную усечённую четырёхугольную пирамиду можно вписать сферу. Рассмотрим сечение пирамиды плоскостью, проходящей через апофемы противоположных боковых граней. Это сечение является равнобедренной трапецией, в которую вписана окружность (большое сечение вписанной сферы). Для четырёхугольника, в который можно вписать окружность (касательный четырёхугольник), суммы длин противоположных сторон равны. Пусть \(a\) — апофема пирамиды, \(b_1\) и \(b_2\) — длины сторон оснований боковой грани (которые являются сторонами верхнего и нижнего оснований пирамиды соответственно). В рассматриваемом сечении, сторонами являются две апофемы и два отрезка, равные сторонам оснований. Сумма длин апофем равна \(a + a = 2a\). Сумма длин сторон оснований боковой грани равна \(b_1 + b_2\). Так как в этот четырёхугольник можно вписать окружность, то \(2a = b_1 + b_2\). Отсюда следует, что \(a = \frac{b_1 + b_2}{2}\). Таким образом, апофема пирамиды равна полусумме сторон оснований её боковой грани.
По условию задачи нам дана правильная усечённая четырёхугольная пирамида, в которую можно вписать сферу. Правильная усечённая четырёхугольная пирамида имеет в основаниях квадраты, а её боковые грани являются равными равнобедренными трапециями. Сфера может быть вписана в усечённую пирамиду тогда и только тогда, когда в сечение пирамиды плоскостью, проходящей через оси симметрии противоположных боковых граней (которые являются апофемами этих граней), можно вписать окружность.
Рассмотрим такое сечение. Оно представляет собой равнобедренную трапецию, боковыми сторонами которой являются апофемы противоположных боковых граней пирамиды, а основаниями — отрезки, соединяющие середины сторон оснований пирамиды. Пусть \(h_a\) — длина апофемы пирамиды. Тогда боковые стороны сечения имеют длину \(h_a\). Пусть \(a_1\) — длина стороны верхнего основания пирамиды, и \(a_2\) — длина стороны нижнего основания пирамиды. Отрезок, соединяющий середины сторон верхнего основания, имеет длину \(a_1\). Отрезок, соединяющий середины сторон нижнего основания, имеет длину \(a_2\). Таким образом, сечение представляет собой равнобедренную трапецию с боковыми сторонами длиной \(h_a\) и основаниями длиной \(a_1\) и \(a_2\).
Поскольку в эту трапецию можно вписать окружность (которая является большим кругом вписанной в пирамиду сферы), то эта трапеция является описанным четырёхугольником. Свойство описанного четырёхугольника гласит, что суммы длин противоположных сторон равны. Для нашей трапеции это означает, что сумма длин боковых сторон равна сумме длин оснований. То есть, \(h_a + h_a = a_1 + a_2\).
Упрощая это уравнение, получаем \(2h_a = a_1 + a_2\).
Разделив обе части уравнения на 2, находим \(h_a = \frac{a_1 + a_2}{2}\).
Длины сторон оснований боковой грани усечённой пирамиды равны длинам сторон оснований самой пирамиды. То есть, если боковая грань является трапецией со сторонами \(c\), \(a_1\), \(c\), \(a_2\), где \(c\) — боковая сторона трапеции (не апофема боковой грани), то \(a_1\) и \(a_2\) — это длины сторон оснований пирамиды. Апофема пирамиды является высотой боковой грани, то есть высотой этой трапеции. В контексте боковой грани как равнобедренной трапеции, её параллельные стороны имеют длины, равные сторонам оснований пирамиды. Если обозначить стороны оснований боковой грани как \(M_1N_1\) и \(MN\), то апофема пирамиды (например, \(NN_1\)) равна \(\frac{M_1N_1 + MN}{2}\), что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.