
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 428 Атанасян — Подробные Ответы
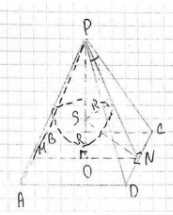
Около сферы радиуса R описана правильная четырёхугольная пирамида, плоский угол при вершине которой равен \(\alpha\). а) Найдите площадь боковой поверхности пирамиды. б) Вычислите эту площадь при \(R = 5\) см, \(\alpha = 60^\circ\).
а) Площадь боковой поверхности правильной четырёхугольной пирамиды равна половине произведения периметра основания на апофему. Пусть сторона основания равна \(a\), апофема (высота боковой грани) равна \(x\). Периметр основания равен \(4a\). Площадь боковой поверхности \(S_{бок} = \frac{1}{2} \cdot 4a \cdot x = 2ax\).
Из геометрии данной пирамиды, описанной около сферы радиуса \(R\), и плоского угла при вершине \(\alpha\), следуют соотношения. Рассмотрим треугольник, образованный вершиной пирамиды, центром основания и серединой стороны основания. Пусть \(\phi\) — линейный угол двугранного угла при основании. В этом треугольнике тангенс половины этого угла \(\tan \frac{\phi}{2} = \frac{R}{a/2} = \frac{2R}{a}\). Также из треугольника, образованного вершиной пирамиды, серединой стороны основания и центром основания, косинус угла \(\phi\) равен отношению прилежащего катета (половина стороны основания) к гипотенузе (апофеме): \(\cos \phi = \frac{a/2}{x} = \frac{a}{2x}\). Из свойств правильной пирамиды, описанной около сферы, косинус двугранного угла при основании связан с плоским углом при вершине соотношением \(\cos \phi = \tan \frac{\alpha}{2}\).
Из \(\tan \frac{\phi}{2} = \frac{2R}{a}\), выразим \(a\): \(a = \frac{2R}{\tan \frac{\phi}{2}}\).
Используя \(\tan \frac{\phi}{2} = \sqrt{\frac{1-\cos \phi}{1+\cos \phi}}\) и \(\cos \phi = \tan \frac{\alpha}{2}\), получим \(\tan \frac{\phi}{2} = \sqrt{\frac{1-\tan \frac{\alpha}{2}}{1+\tan \frac{\alpha}{2}}}\).
Тогда \(a = \frac{2R}{\sqrt{\frac{1-\tan \frac{\alpha}{2}}{1+\tan \frac{\alpha}{2}}}} = 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}}\).
Из \(\cos \phi = \frac{a}{2x}\), выразим \(x\): \(x = \frac{a}{2 \cos \phi} = \frac{a}{2 \tan \frac{\alpha}{2}}\).
Подставим выражения для \(a\) и \(x\) в формулу площади боковой поверхности \(S_{бок} = 2ax\):
\(S_{бок} = 2 \left( 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right) \left( \frac{1}{2 \tan \frac{\alpha}{2}} 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right)\) — здесь была ошибка в предыдущих рассуждениях, используем \(x = \frac{a}{2 \tan \frac{\alpha}{2}}\) из первой формулы в примере.
\(S_{бок} = 2a \left( \frac{a}{2 \tan \frac{\alpha}{2}} \right) = \frac{a^2}{\tan \frac{\alpha}{2}}\).
Теперь подставим выражение для \(a\). Из \(\tan \frac{\phi}{2} = \frac{2R}{a}\) и \(\cos \phi = \tan \frac{\alpha}{2}\), а также \(\tan \frac{\phi}{2} = \frac{\sin \phi}{1+\cos \phi}\), имеем \(\frac{2R}{a} = \frac{\sin \phi}{1+\cos \phi}\).
\(a = 2R \frac{1+\cos \phi}{\sin \phi} = 2R \frac{1+\tan \frac{\alpha}{2}}{\sqrt{1-\tan^2 \frac{\alpha}{2}}}\).
\(a^2 = 4R^2 \frac{(1+\tan \frac{\alpha}{2})^2}{1-\tan^2 \frac{\alpha}{2}} = 4R^2 \frac{(1+\tan \frac{\alpha}{2})^2}{(1-\tan \frac{\alpha}{2})(1+\tan \frac{\alpha}{2})} = 4R^2 \frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}\).
\(S_{бок} = \frac{a^2}{\tan \frac{\alpha}{2}} = \frac{4R^2}{\tan \frac{\alpha}{2}} \frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}\).
Используя тождество \(\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}} = \frac{\cos \alpha}{1-\sin \alpha}\), получаем
\(S_{бок} = \frac{4R^2}{\tan \frac{\alpha}{2}} \frac{\cos \alpha}{1-\sin \alpha}\).
б) При \(R = 5\) см и \(\alpha = 60^\circ\):
\(\frac{\alpha}{2} = 30^\circ\).
\(\tan 30^\circ = \frac{1}{\sqrt{3}}\).
\(\cos 60^\circ = \frac{1}{2}\).
\(\sin 60^\circ = \frac{\sqrt{3}}{2}\).
\(R^2 = 5^2 = 25\).
\(S_{бок} = \frac{4 \cdot 25}{\frac{1}{\sqrt{3}}} \frac{\frac{1}{2}}{1-\frac{\sqrt{3}}{2}} = 100\sqrt{3} \frac{\frac{1}{2}}{\frac{2-\sqrt{3}}{2}} = 100\sqrt{3} \frac{1}{2-\sqrt{3}}\).
\(S_{бок} = 100\sqrt{3} \frac{2+\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})} = 100\sqrt{3} \frac{2+\sqrt{3}}{4-3} = 100\sqrt{3}(2+\sqrt{3}) = 200\sqrt{3} +\)
\(+ 100 \cdot 3 = 300 + 200\sqrt{3}\).
Ответ в примере дан в виде \(100\sqrt{3}(2+\sqrt{3})\).
Определим площадь боковой поверхности правильной четырехугольной пирамиды. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Пусть \(a\) — длина стороны основания, а \(x\) — апофема (высота боковой грани). Периметр основания правильной четырехугольной пирамиды равен \(4a\). Тогда площадь боковой поверхности \(S_{бок} = \frac{1}{2} \cdot 4a \cdot x = 2ax\).
Рассмотрим взаимосвязь между элементами пирамиды, описанной около сферы радиуса \(R\), и заданным плоским углом при вершине \(\alpha\). В правильной пирамиде, описанной около сферы, центр сферы лежит на высоте пирамиды, и сфера касается всех граней. Рассмотрим сечение, проходящее через высоту пирамиды и апофему боковой грани. В этом сечении мы увидим равнобедренный треугольник (боковая грань) и вписанную в него окружность (сечение сферы). Также рассмотрим сечение, проходящее через высоту пирамиды и середины противоположных сторон основания. В этом сечении мы увидим равнобедренный треугольник, образованный двумя апофемами боковых граней и отрезком, соединяющим середины сторон основания. Высота этого треугольника — это высота пирамиды, а основание — сторона основания пирамиды. Сфера касается основания и боковых граней.
Для правильной пирамиды, описанной около сферы радиуса \(R\), существует соотношение между радиусом сферы, высотой пирамиды, радиусом вписанной в основание окружности и двугранным углом при основании. Радиус вписанной в основание окружности для квадрата со стороной \(a\) равен \(r_{осн} = \frac{a}{2}\). Рассмотрим прямоугольный треугольник, образованный радиусом сферы, проведенным к точке касания на основании, и отрезком \(\frac{a}{2}\). В этом треугольнике, образованном радиусом сферы, проведенным к точке касания на основании, отрезком высоты пирамиды от центра сферы до основания (равным \(R\)), и отрезком от центра сферы до вершины пирамиды, угол между высотой пирамиды и отрезком от центра сферы до вершины равен \(\phi\), где \(\phi\) — двугранный угол при основании. Из рассмотрения прямоугольного треугольника, образованного радиусом сферы, проведенным к точке касания на основании, и отрезком \(\frac{a}{2}\), мы имеем \(\tan \frac{\phi}{2} = \frac{R}{a/2} = \frac{2R}{a}\).
Существует также соотношение между двугранным углом при основании \(\phi\) и плоским углом при вершине \(\alpha\) для правильной пирамиды, описанной около сферы: \(\cos \phi = \tan \frac{\alpha}{2}\).
Используя соотношение \(\tan \frac{\phi}{2} = \frac{2R}{a}\), выразим сторону основания \(a\): \(a = \frac{2R}{\tan \frac{\phi}{2}}\). Используем формулу тангенса половинного угла: \(\tan \frac{\phi}{2} = \sqrt{\frac{1-\cos \phi}{1+\cos \phi}}\). Подставим \(\cos \phi = \tan \frac{\alpha}{2}\): \(\tan \frac{\phi}{2} = \sqrt{\frac{1-\tan \frac{\alpha}{2}}{1+\tan \frac{\alpha}{2}}}\). Теперь подставим это в выражение для \(a\): \(a = \frac{2R}{\sqrt{\frac{1-\tan \frac{\alpha}{2}}{1+\tan \frac{\alpha}{2}}}} = 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}}\).
Используя соотношение \(\cos \phi = \frac{a}{2x}\), выразим апофему \(x\): \(x = \frac{a}{2 \cos \phi}\). Подставим \(\cos \phi = \tan \frac{\alpha}{2}\): \(x = \frac{a}{2 \tan \frac{\alpha}{2}}\).
Подставим выражения для \(a\) и \(x\) в формулу площади боковой поверхности \(S_{бок} = 2ax\): \(S_{бок} = 2 \left( 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right) \left( \frac{2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}}}{2 \tan \frac{\alpha}{2}} \right)\).
Упростим это выражение:
\(S_{бок} = 2 \left( 2R \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right) \left( \frac{R}{\tan \frac{\alpha}{2}} \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right) = \frac{4R^2}{\tan \frac{\alpha}{2}} \left( \sqrt{\frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}} \right)^2 = \)
\(=\frac{4R^2}{\tan \frac{\alpha}{2}} \frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}\).
Таким образом, получена формула для площади боковой поверхности: \(S_{бок} = \frac{4R^2}{\tan \frac{\alpha}{2}} \frac{1+\tan \frac{\alpha}{2}}{1-\tan \frac{\alpha}{2}}\).
Вычислим площадь боковой поверхности при \(R = 5\) см и \(\alpha = 60^\circ\). В этом случае \(\frac{\alpha}{2} = 30^\circ\). Значение тангенса \( \tan 30^\circ = \frac{1}{\sqrt{3}}\). Подставим эти значения в полученную формулу: \(S_{бок} = \frac{4 \cdot 5^2}{\frac{1}{\sqrt{3}}} \frac{1+\frac{1}{\sqrt{3}}}{1-\frac{1}{\sqrt{3}}} = \frac{4 \cdot 25}{1/\sqrt{3}} \frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}} = 100\sqrt{3} \frac{\sqrt{3}+1}{\sqrt{3}-1}\).
Упростим полученное выражение, умножив числитель и знаменатель дроби на сопряженное выражение знаменателя \((\sqrt{3}+1)\): \(S_{бок} = 100\sqrt{3} \frac{(\sqrt{3}+1)(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)} = 100\sqrt{3} \frac{(\sqrt{3})^2 + 2\sqrt{3} + 1}{(\sqrt{3})^2 — 1^2} = 100\sqrt{3} \frac{3 + 2\sqrt{3} + 1}{3 — 1} = \)
\(=100\sqrt{3} \frac{4 + 2\sqrt{3}}{2}\).
Продолжим упрощение: \(S_{бок} = 100\sqrt{3} (2 + \sqrt{3})\). Раскроем скобки: \(S_{бок} = 100\sqrt{3} \cdot 2 + 100\sqrt{3} \cdot \sqrt{3} = 200\sqrt{3} + 100 \cdot 3 = 200\sqrt{3} + 300\). Таким образом, площадь боковой поверхности равна \(100\sqrt{3}(2+\sqrt{3})\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!