Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 427 Атанасян — Подробные Ответы
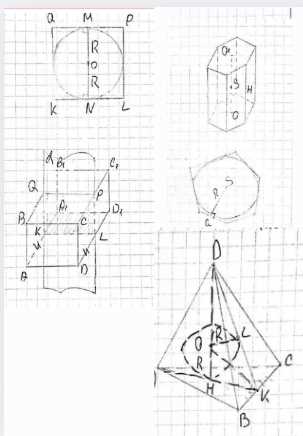
Найдите площадь полной поверхности описанного около сферы радиуса R многогранника, если этот многогранник: а) куб; б) правильная шестиугольная призма; в) правильный тетраэдр.
а) Пусть ребро куба равно \(a\), тогда \(a = 2R\). Площадь одной грани равна \(a^2\) или \((2R)^2 = 4R^2\). Площадь полной поверхности куба равна \(6 \cdot 4R^2 = 24R^2\).
б) Высота призмы равна диаметру сферы, то есть \(H = 2R\). Пусть сторона правильного шестиугольника в основании равна \(a\). Расстояние от центра основания до середины стороны равно радиусу вписанной окружности основания, которое равно радиусу сферы \(R\). Для правильного шестиугольника это расстояние равно \(a \frac{\sqrt{3}}{2}\), поэтому \(R = a \frac{\sqrt{3}}{2}\), откуда \(a = \frac{2R}{\sqrt{3}}\). Площадь боковой грани (прямоугольника) равна \(H \cdot a = 2R \cdot \frac{2R}{\sqrt{3}} = \frac{4R^2}{\sqrt{3}}\). Площадь боковой поверхности призмы равна \(6 \cdot \frac{4R^2}{\sqrt{3}} = \frac{24R^2}{\sqrt{3}} = 8\sqrt{3}R^2\). Площадь основания (правильного шестиугольника) равна \(6 \cdot \frac{\sqrt{3}}{4} a^2 = 6 \cdot \frac{\sqrt{3}}{4} (\frac{2R}{\sqrt{3}})^2 = 6 \cdot \frac{\sqrt{3}}{4} \frac{4R^2}{3} = 2\sqrt{3}R^2\). Площадь полной поверхности призмы равна \(S_{бок} + 2 S_{осн} = 8\sqrt{3}R^2 + 2 \cdot 2\sqrt{3}R^2 = 8\sqrt{3}R^2 + 4\sqrt{3}R^2 = 12\sqrt{3}R^2\).
в) Пусть ребро правильного тетраэдра равно \(a\). Высота грани тетраэдра \(DK = \frac{a\sqrt{3}}{2}\). Радиус окружности, вписанной в основание тетраэдра, \(HK = \frac{1}{3} DK = \frac{1}{3} \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{6}\). Расстояние от центра сферы до грани тетраэдра равно радиусу сферы \(R\). В правильном тетраэдре центр вписанной сферы совпадает с центром тетраэдра. Высота тетраэдра \(H = \frac{a\sqrt{2}}{\sqrt{3}}\). Центр сферы делит высоту тетраэдра в отношении 1:3, считая от основания. Радиус вписанной сферы \(R = \frac{1}{4} H = \frac{1}{4} \frac{a\sqrt{2}}{\sqrt{3}} = \frac{a\sqrt{2}}{4\sqrt{3}}\). Отсюда \(a = \frac{4\sqrt{3}R}{\sqrt{2}} = \frac{4\sqrt{6}R}{2} = 2\sqrt{6}R\). Площадь одной грани (равностороннего треугольника) равна \(S_{грани} = \frac{a^2\sqrt{3}}{4} = \frac{(2\sqrt{6}R)^2\sqrt{3}}{4} = \frac{24R^2\sqrt{3}}{4} = 6\sqrt{3}R^2\). Площадь полной поверхности тетраэдра равна \(4 \cdot S_{грани} = 4 \cdot 6\sqrt{3}R^2 = 24\sqrt{3}R^2\).
а) Рассмотрим куб, описанный около сферы радиуса \(R\). В этом случае диаметр сферы равен длине ребра куба. Пусть ребро куба равно \(a\). Тогда \(a = 2R\). Площадь одной грани куба, которая является квадратом со стороной \(a\), равна \(a^2\). Подставляя \(a = 2R\), получаем площадь грани \((2R)^2 = 4R^2\). Куб имеет шесть одинаковых граней, поэтому площадь полной поверхности куба равна сумме площадей всех его граней, то есть \(6 \cdot 4R^2 = 24R^2\).
б) Рассмотрим правильную шестиугольную призму, описанную около сферы радиуса \(R\). Высота призмы равна диаметру сферы, так как сфера касается верхнего и нижнего оснований. Высота призмы \(H = 2R\). Сфера также касается всех боковых граней призмы. Это означает, что радиус окружности, вписанной в основание призмы (правильный шестиугольник), равен радиусу сферы \(R\). Пусть сторона правильного шестиугольника в основании равна \(a\). Радиус вписанной окружности правильного шестиугольника со стороной \(a\) равен \(r_{in} = a \frac{\sqrt{3}}{2}\). Поскольку \(r_{in} = R\), имеем \(R = a \frac{\sqrt{3}}{2}\), откуда выражаем сторону основания \(a = \frac{2R}{\sqrt{3}}\). Боковая грань призмы является прямоугольником с высотой \(H\) и шириной \(a\). Площадь одной боковой грани равна \(H \cdot a = 2R \cdot \frac{2R}{\sqrt{3}} = \frac{4R^2}{\sqrt{3}}\). Поскольку призма шестиугольная, у нее шесть боковых граней. Площадь боковой поверхности призмы равна \(6 \cdot \frac{4R^2}{\sqrt{3}} = \frac{24R^2}{\sqrt{3}} = 8\sqrt{3}R^2\). Основание призмы — правильный шестиугольник. Площадь правильного шестиугольника можно найти как сумму площадей шести равносторонних треугольников со стороной \(a\). Площадь одного такого треугольника равна \(\frac{\sqrt{3}}{4} a^2\). Площадь основания равна \(6 \cdot \frac{\sqrt{3}}{4} a^2 = \frac{3\sqrt{3}}{2} a^2\). Подставляя \(a = \frac{2R}{\sqrt{3}}\), получаем площадь основания \( \frac{3\sqrt{3}}{2} (\frac{2R}{\sqrt{3}})^2 = \frac{3\sqrt{3}}{2} \frac{4R^2}{3} = 2\sqrt{3}R^2 \). Площадь полной поверхности призмы равна сумме площади боковой поверхности и площадей двух оснований: \(S_{полн} = S_{бок} + 2 S_{осн} = 8\sqrt{3}R^2 + 2 \cdot 2\sqrt{3}R^2 = 8\sqrt{3}R^2 + 4\sqrt{3}R^2 = 12\sqrt{3}R^2\).
в) Рассмотрим правильный тетраэдр, описанный около сферы радиуса \(R\). Все ребра правильного тетраэдра равны. Пусть длина ребра тетраэдра равна \(a\). Сфера касается всех четырех граней тетраэдра. Центр вписанной сферы находится на высоте тетраэдра. Рассмотрим одну грань, например, \(\triangle ABC\), и высоту этой грани \(DK\), где \(K\) — середина ребра \(BC\). В равностороннем треугольнике высота \(DK = \sqrt{a^2 — (\frac{a}{2})^2} = \sqrt{a^2 — \frac{a^2}{4}} = \sqrt{\frac{3a^2}{4}} = \frac{a\sqrt{3}}{2}\). Рассмотрим основание \(\triangle ABC\). Центр вписанной в основание окружности \(H\) является точкой пересечения медиан (и высот, и биссектрис). Радиус вписанной в основание окружности \(HK\) равен одной трети высоты \(DK\), то есть \(HK = \frac{1}{3} DK = \frac{1}{3} \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{6}\). Угол между гранью \(DBC\) и основанием \(ABC\) (двугранный угол при ребре основания) — это линейный угол \(\angle DKH\). В прямоугольном треугольнике \(\triangle DKH\) (где \(DH\) — высота тетраэдра), \(\cos(\angle DKH) = \frac{HK}{DK} = \frac{a\sqrt{3}/6}{a\sqrt{3}/2} = \frac{a\sqrt{3}}{6} \cdot \frac{2}{a\sqrt{3}} = \frac{2}{6} = \frac{1}{3}\). Тогда \(\sin(\angle DKH) = \sqrt{1 — \cos^2(\angle DKH)} = \sqrt{1 — (\frac{1}{3})^2} = \sqrt{1 — \frac{1}{9}} = \sqrt{\frac{8}{9}} = \frac{2\sqrt{2}}{3}\). Рассмотрим треугольник, образованный центром сферы \(O\), точкой касания сферы с основанием \(N\) (которая совпадает с \(H\)), и точкой \(K\) на ребре основания. В этом треугольнике \(\triangle ONK\) угол \(\angle OKN\) равен половине двугранного угла \(\angle DKH\). Катет \(ON\) равен радиусу сферы \(R\), а катет \(NK\) равен радиусу вписанной в основание окружности \(HK\). Тогда \(\tan(\angle OKN) = \tan(\frac{\angle DKH}{2}) = \frac{ON}{NK} = \frac{R}{HK}\). Используем формулу тангенса половинного угла: \(\tan(\frac{\alpha}{2}) = \frac{\sin\alpha}{1+\cos\alpha}\). \(\tan(\frac{\angle DKH}{2}) = \frac{2\sqrt{2}/3}{1 + 1/3} = \frac{2\sqrt{2}/3}{4/3} = \frac{2\sqrt{2}}{4} = \frac{\sqrt{2}}{2}\). Приравниваем \(\frac{R}{HK} = \frac{\sqrt{2}}{2}\). Подставляем \(HK = \frac{a\sqrt{3}}{6}\): \(\frac{R}{a\sqrt{3}/6} = \frac{\sqrt{2}}{2}\). \(\frac{6R}{a\sqrt{3}} = \frac{\sqrt{2}}{2}\). \(12R = a\sqrt{3}\sqrt{2} = a\sqrt{6}\). Выражаем \(a\): \(a = \frac{12R}{\sqrt{6}} = \frac{12R\sqrt{6}}{6} = 2\sqrt{6}R\). Площадь одной грани тетраэдра (равностороннего треугольника со стороной \(a\)) равна \(S_{грани} = \frac{\sqrt{3}}{4} a^2\). Подставляем \(a = 2\sqrt{6}R\): \(S_{грани} = \frac{\sqrt{3}}{4} (2\sqrt{6}R)^2 = \frac{\sqrt{3}}{4} (4 \cdot 6 R^2) = \frac{\sqrt{3}}{4} \cdot 24R^2 = 6\sqrt{3}R^2\). Правильный тетраэдр имеет четыре одинаковые грани. Площадь полной поверхности тетраэдра равна \(4 \cdot S_{грани} = 4 \cdot 6\sqrt{3}R^2 = 24\sqrt{3}R^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.