Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 426 Атанасян — Подробные Ответы
Докажите, что центр сферы, вписанной в правильную пирамиду, лежит на высоте этой пирамиды.
В правильной пирамиде рассмотрим сечение, проходящее через высоту SD и апофему боковой грани SE. В треугольник SDE впишем полуокружность с центром на высоте SD, касающуюся сторон DE и SE. При вращении этого сечения вокруг высоты SD, полуокружность описывает сферу, которая будет касаться основания пирамиды в точке D и всех боковых граней, поскольку SE при вращении описывает боковые грани, а DE описывает окружность, вписанную в основание. Так как центр этой полуокружности лежит на высоте SD, то и центр вписанной сферы лежит на высоте пирамиды.
Рассмотрим правильную пирамиду с вершиной \(S\) и основанием. Пусть \(SD\) будет высотой этой пирамиды, где точка \(D\) является центром основания. Поскольку пирамида правильная, основание является правильным многоугольником, и точка \(D\) также является центром вписанной и описанной окружностей основания.
Возьмем сечение пирамиды, проходящее через высоту \(SD\) и апофему \(SE\) одной из боковых граней, где \(E\) — середина стороны основания. В правильной пирамиде отрезок \(DE\), соединяющий центр основания \(D\) с серединой стороны основания \(E\), является радиусом вписанной окружности основания и перпендикулярен этой стороне. Треугольник \(SDE\) является прямоугольным с прямым углом при вершине \(D\), так как высота \(SD\) перпендикулярна плоскости основания. Отрезок \(SE\) является апофемой боковой грани.
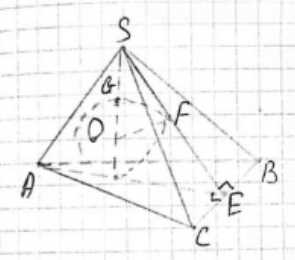
В прямоугольный треугольник \(SDE\) впишем полуокружность \(DFG\) таким образом, чтобы ее центр \(Q\) лежал на катете \(SD\), а сама полуокружность касалась катета \(DE\) и гипотенузы \(SE\). Такую полуокружность можно построить, и ее центр будет равноудален от прямых, содержащих \(DE\) и \(SE\).
Теперь представим, что мы вращаем этот прямоугольный треугольник \(SDE\) вместе с вписанной в него полуокружностью \(DFG\) вокруг оси, совпадающей с высотой \(SD\).
При вращении треугольника \(SDE\) вокруг \(SD\), катет \(DE\) описывает окружность в плоскости основания. Эта окружность является вписанной окружностью основания пирамиды, поскольку \(D\) — центр основания, а \(DE\) — радиус вписанной окружности, перпендикулярный стороне основания. Гипотенуза \(SE\) при вращении вокруг \(SD\) описывает боковую поверхность пирамиды.
Полуокружность \(DFG\), вписанная в треугольник \(SDE\) с центром \(Q\) на \(SD\) и касающаяся \(DE\) и \(SE\), при вращении вокруг оси \(SD\) опишет сферу.
Поскольку полуокружность касалась отрезка \(DE\), который при вращении описывает вписанную окружность основания, сфера, образованная вращением полуокружности, будет касаться плоскости основания пирамиды по этой вписанной окружности. Для правильной пирамиды точка касания сферы с основанием будет в центре вписанной окружности, то есть в точке \(D\).
Поскольку полуокружность касалась отрезка \(SE\), который при вращении описывает боковую поверхность пирамиды (совокупность всех апофем боковых граней), сфера, образованная вращением полуокружности, будет касаться всех боковых граней пирамиды.
Таким образом, сфера, образованная вращением полуокружности \(DFG\) вокруг \(SD\), является сферой, вписанной в пирамиду, так как она касается основания и всех боковых граней. Центр этой сферы совпадает с центром \(Q\) вращающейся полуокружности. По построению, центр \(Q\) полуокружности лежит на катете \(SD\), который является высотой пирамиды. Следовательно, центр сферы, вписанной в правильную пирамиду, лежит на высоте этой пирамиды.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.