Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 425 Атанасян — Подробные Ответы
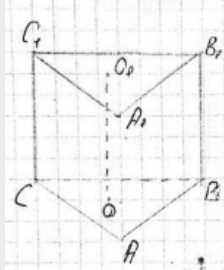
Докажите, что если в правильную призму можно вписать сферу, то центром сферы является середина отрезка, соединяющего центры оснований этой призмы.
Доказательство: Центр сферы, вписанной в правильную призму, равноудален от всех ее граней. Поскольку сфера касается верхнего и нижнего оснований, ее центр находится в плоскости, параллельной основаниям и проходящей ровно посередине между ними. Эта плоскость пересекает боковые ребра в их серединах. Сечение призмы этой плоскостью является многоугольником, центром которого в силу симметрии является точка на отрезке, соединяющем центры оснований призмы. Поскольку плоскость находится посередине между основаниями, эта точка является серединой отрезка, соединяющего центры оснований, что и требовалось доказать.
Пусть дана правильная призма и сфера, вписанная в эту призму. Это означает, что сфера касается всех граней призмы: обоих оснований и всех боковых граней.
По определению, центр вписанной сферы равноудален от всех граней, которых она касается. Обозначим центр сферы как \(O_s\).
Сфера касается верхнего и нижнего оснований призмы. Расстояние от центра сферы до верхнего основания равно радиусу сферы \(r\), и расстояние от центра сферы до нижнего основания также равно радиусу сферы \(r\). Это возможно только в том случае, если центр сферы \(O_s\) лежит в плоскости, которая параллельна обоим основаниям и находится ровно на равном расстоянии от них. Если высота призмы равна \(h\), то эта плоскость находится на расстоянии \(h/2\) от каждого основания.
Эта плоскость пересекает правильную призму. Поскольку плоскость параллельна основаниям, сечением призмы этой плоскостью будет многоугольник, конгруэнтный основаниям призмы. Так как призма правильная, ее основания являются правильными многоугольниками. Следовательно, сечение также является правильным многоугольником.
Центр сферы \(O_s\) лежит в плоскости этого сечения.
Рассмотрим отрезок \(OO_1\), соединяющий центры оснований призмы (где \(O\) — центр нижнего основания, а \(O_1\) — центр верхнего основания). В правильной призме этот отрезок перпендикулярен плоскостям оснований и проходит через геометрические центры оснований.
Плоскость, в которой лежит центр сферы \(O_s\), параллельна основаниям и находится на середине высоты призмы. Эта плоскость пересекает отрезок \(OO_1\). Точка пересечения этой плоскости с отрезком \(OO_1\) является серединой этого отрезка, поскольку плоскость делит высоту призмы пополам.
Центр правильного многоугольника, являющегося сечением призмы этой плоскостью, совпадает с точкой пересечения отрезка \(OO_1\) с этой плоскостью. Поскольку центр сферы \(O_s\) лежит в плоскости сечения и равноудален от всех боковых граней (которые пересекаются этой плоскостью по сторонам правильного многоугольника сечения), центр сферы \(O_s\) совпадает с центром этого правильного многоугольника сечения.
Таким образом, центр сферы \(O_s\) лежит на отрезке \(OO_1\) и совпадает с его серединой. Это и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.