
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 423 Атанасян — Подробные Ответы
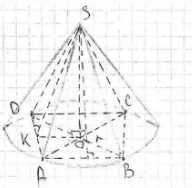
В конус высотой 12 см вписана пирамида, основанием которой является прямоугольник со сторонами 6 см и 8 см. Найдите отношение площадей полных поверхностей пирамиды и конуса.
Диагональ основания пирамиды равна \(BD = \sqrt{8^2 + 6^2} = \sqrt{100} = 10\) см. Радиус основания конуса равен \(r = \frac{BD}{2} = 5\) см. Площадь основания конуса равна \(S_{осн\_конуса} = \pi r^2 = \pi \cdot 5^2 = 25\pi\) см². Образующая конуса (и ребро пирамиды) равна \(L = \sqrt{h^2 + r^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13\) см. Площадь боковой поверхности конуса равна \(S_{бок\_конуса} = \pi r L = \pi \cdot 5 \cdot 13 = 65\pi\) см². Полная площадь поверхности конуса равна \(S_{полн\_конуса} = S_{осн\_конуса} + S_{бок\_конуса} = 25\pi + 65\pi = 90\pi\) см².
Площадь основания пирамиды равна \(S_{осн\_пирамиды} = 8 \cdot 6 = 48\) см². Апофема боковой грани над стороной 8 см равна \(SL = \sqrt{h^2 + (\frac{6}{2})^2} = \sqrt{12^2 + 3^2} = \sqrt{144 + 9} = \sqrt{153} = 3\sqrt{17}\) см. Площадь двух боковых граней над сторонами 8 см равна \(2 \cdot \frac{1}{2} \cdot 8 \cdot 3\sqrt{17} = 24\sqrt{17}\) см². Апофема боковой грани над стороной 6 см равна \(SK = \sqrt{h^2 + (\frac{8}{2})^2} = \sqrt{12^2 + 4^2} = \sqrt{144 + 16} = \sqrt{160} = 4\sqrt{10}\) см. Площадь двух боковых граней над сторонами 6 см равна \(2 \cdot \frac{1}{2} \cdot 6 \cdot 4\sqrt{10} = 24\sqrt{10}\) см². Полная площадь поверхности пирамиды равна \(S_{полн\_пирамиды} = S_{осн\_пирамиды} + S_{бок\_пирамиды} = 48 + 24\sqrt{17} + 24\sqrt{10} =\)
\(= 24(2 + \sqrt{17} + \sqrt{10})\) см².
Отношение площадей полных поверхностей пирамиды и конуса равно \(\frac{S_{полн\_пирамиды}}{S_{полн\_конуса}} = \frac{24(2 + \sqrt{17} + \sqrt{10})}{90\pi} = \frac{4(2 + \sqrt{17} + \sqrt{10})}{15\pi}\).
Диагональ основания пирамиды, которое является прямоугольником со сторонами 8 см и 6 см, находится по теореме Пифагора как гипотенуза прямоугольного треугольника с катетами 8 см и 6 см. Диагональ \(BD = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10\) см. Эта диагональ является диаметром основания конуса. Радиус основания конуса равен половине диаметра, то есть \(r = \frac{10}{2} = 5\) см.
Площадь основания конуса вычисляется по формуле \(S_{осн\_конуса} = \pi r^2\). Подставляя значение радиуса, получаем \(S_{осн\_конуса} = \pi \cdot 5^2 = 25\pi\) см².
Образующая конуса \(L\) является гипотенузой прямоугольного треугольника, образованного высотой конуса \(h = 12\) см и радиусом основания \(r = 5\) см. По теореме Пифагора, \(L = \sqrt{h^2 + r^2} = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13\) см. Эта образующая также является длиной всех боковых ребер вписанной пирамиды.
Площадь боковой поверхности конуса вычисляется по формуле \(S_{бок\_конуса} = \pi r L\). Подставляя значения радиуса и образующей, получаем \(S_{бок\_конуса} = \pi \cdot 5 \cdot 13 = 65\pi\) см².
Полная площадь поверхности конуса равна сумме площади основания и площади боковой поверхности: \(S_{полн\_конуса} = S_{осн\_конуса} + S_{бок\_конуса} = 25\pi + 65\pi = 90\pi\) см².
Площадь основания пирамиды, являющегося прямоугольником со сторонами 8 см и 6 см, равна произведению его сторон: \(S_{осн\_пирамиды} = 8 \cdot 6 = 48\) см².
Для вычисления площадей боковых граней пирамиды необходимо найти их апофемы. Боковые грани являются треугольниками. Рассмотрим грани, опирающиеся на стороны длиной 8 см. Расстояние от центра основания (основания высоты пирамиды) до этих сторон равно половине длины другой стороны прямоугольника, то есть \(\frac{6}{2} = 3\) см. Апофема \(SL\) такой грани является гипотенузой прямоугольного треугольника с катетами, равными высоте пирамиды \(h = 12\) см и расстоянию от центра до стороны 3 см. По теореме Пифагора, \(SL = \sqrt{12^2 + 3^2} = \sqrt{144 + 9} = \sqrt{153} = \sqrt{9 \cdot 17} = 3\sqrt{17}\) см. Площадь двух таких граней равна \(2 \cdot \frac{1}{2} \cdot 8 \cdot 3\sqrt{17} = 24\sqrt{17}\) см².
Рассмотрим грани, опирающиеся на стороны длиной 6 см. Расстояние от центра основания до этих сторон равно половине длины другой стороны прямоугольника, то есть \(\frac{8}{2} = 4\) см. Апофема \(SK\) такой грани является гипотенузой прямоугольного треугольника с катетами, равными высоте пирамиды \(h = 12\) см и расстоянию от центра до стороны 4 см. По теореме Пифагора, \(SK = \sqrt{12^2 + 4^2} = \sqrt{144 + 16} = \sqrt{160} = \sqrt{16 \cdot 10} = 4\sqrt{10}\) см. Площадь двух таких граней равна \(2 \cdot \frac{1}{2} \cdot 6 \cdot 4\sqrt{10} = 24\sqrt{10}\) см².
Полная площадь поверхности пирамиды равна сумме площади основания и площадей всех боковых граней: \(S_{полн\_пирамиды} = S_{осн\_пирамиды} + 24\sqrt{17} + 24\sqrt{10} = 48 + 24\sqrt{17} + 24\sqrt{10}\) см². Эту площадь можно представить как \(24(2 + \sqrt{17} + \sqrt{10})\) см².
Отношение площадей полных поверхностей пирамиды и конуса равно \(\frac{S_{полн\_пирамиды}}{S_{полн\_конуса}}\). Подставляя найденные значения, получаем отношение \(\frac{24(2 + \sqrt{17} + \sqrt{10})}{90\pi}\). Сокращая числитель и знаменатель на 6, получаем \(\frac{4(2 + \sqrt{17} + \sqrt{10})}{15\pi}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!