Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 422 Атанасян — Подробные Ответы
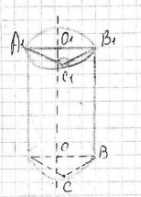
Докажите, что если одна из граней вписанной в цилиндр треугольной призмы проходит через ось цилиндра, то две другие грани взаимно перпендикулярны.
Пусть грань \(ABB_1A_1\) проходит через ось цилиндра.
Тогда AB является диаметром основания. Поскольку треугольник ABC вписан в окружность основания и AB — диаметр, угол \(\angle ACB = 90^\circ\). Образующая \(CC_1\) перпендикулярна плоскости основания. Следовательно, \(BC \perp CC_1\). Так как \(\angle ACB = 90^\circ\), \(BC \perp AC\). Поскольку прямая BC перпендикулярна двум пересекающимся прямым AC и \(CC_1\) в плоскости \(ACC_1A_1\), прямая BC перпендикулярна плоскости \(ACC_1A_1\). Плоскость \(BCC_1B_1\) содержит прямую BC, которая перпендикулярна плоскости \(ACC_1A_1\). Следовательно, плоскость \(BCC_1B_1\) перпендикулярна плоскости \(ACC_1A_1\).
Пусть дана треугольная призма \(ABCA_1B_1C_1\), вписанная в цилиндр, такая что грань \(ABB_1A_1\) проходит через ось цилиндра. Поскольку грань \(ABB_1A_1\) проходит через ось цилиндра, сторона AB треугольника ABC, лежащая в основании призмы, является диаметром окружности основания цилиндра. Треугольник ABC вписан в окружность основания, и его сторона AB является диаметром этой окружности. По свойству угла, опирающегося на диаметр окружности, угол \(\angle ACB\) является прямым, то есть \(\angle ACB = 90^\circ\).
В прямой призме боковые ребра перпендикулярны плоскостям оснований. В данном случае, поскольку призма вписана в цилиндр, ее боковые ребра являются образующими цилиндра и, следовательно, перпендикулярны плоскостям оснований. Таким образом, ребро \(CC_1\) перпендикулярно плоскости основания ABC. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости. Следовательно, \(CC_1\) перпендикулярно прямой BC, которая лежит в плоскости основания ABC. То есть, \(BC \perp CC_1\).
Мы установили, что \(BC \perp AC\) (так как \(\angle ACB = 90^\circ\)) и \(BC \perp CC_1\). Прямые AC и \(CC_1\) лежат в плоскости грани \(ACC_1A_1\) и пересекаются в точке C. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. Следовательно, прямая BC перпендикулярна плоскости \(ACC_1A_1\).
Грань \(BCC_1B_1\) содержит прямую BC. Если плоскость содержит прямую, перпендикулярную другой плоскости, то эти две плоскости взаимно перпендикулярны. Поскольку плоскость \(BCC_1B_1\) содержит прямую BC, которая перпендикулярна плоскости \(ACC_1A_1\), то плоскость \(BCC_1B_1\) перпендикулярна плоскости \(ACC_1A_1\). Таким образом, две другие грани призмы, \(ACC_1A_1\) и \(BCC_1B_1\), взаимно перпендикулярны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.