Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 421 Атанасян — Подробные Ответы
Тело ограничено двумя сферами с общим центром. Докажите, что площадь его сечения плоскостью, проходящей через центры сфер, равна площади сечения плоскостью, касательной к внутренней сфере.
Разные задачи на многогранники, цилиндр, конус и шар
Поясним некоторые термины, которые встречаются в задачах этого раздела. Напомним, что многогранник называется описанным около сферы, если сфера касается всех его граней. При этом сфера называется вписанной в многогранник. Многогранник называется вписанным в сферу, если все его вершины лежат на сфере. При этом сфера называется описанной около многогранника.
Пусть \(R\) — радиус внешней сферы, а \(r\) — радиус внутренней сферы. Сечение плоскостью, проходящей через центр сфер, представляет собой кольцо между двумя концентрическими окружностями радиусов \(R\) и \(r\). Площадь этого кольца равна разности площадей кругов, то есть \(\pi R^2 — \pi r^2 = \pi(R^2 — r^2)\).
Сечение плоскостью, касательной к внутренней сфере, представляет собой круг. Расстояние от центра сфер до этой плоскости равно радиусу внутренней сферы, то есть \(r\). Рассмотрим прямоугольный треугольник, образованный центром сфер, точкой касания плоскости к внутренней сфере и точкой на окружности сечения. Гипотенуза этого треугольника равна радиусу внешней сферы \(R\), один катет равен расстоянию от центра до плоскости \(r\), а другой катет \(x\) является радиусом окружности сечения. По теореме Пифагора имеем \(x^2 + r^2 = R^2\), откуда \(x^2 = R^2 — r^2\). Площадь этого круга равна \(\pi x^2 = \pi(R^2 — r^2)\).
Таким образом, площади обоих сечений равны \(\pi(R^2 — r^2)\), что доказывает утверждение задачи.
Рассмотрим тело, ограниченное двумя концентрическими сферами с общим центром. Пусть радиус внешней сферы равен \(R\), а радиус внутренней сферы равен \(r\), где \(r < R\). Нам необходимо доказать, что площадь сечения этого тела плоскостью, проходящей через центр сфер, равна площади сечения плоскостью, касательной к внутренней сфере.
Сначала рассмотрим случай, когда секущая плоскость проходит через общий центр обеих сфер. В этом случае сечение внешней сферы представляет собой круг радиуса \(R\), а сечение внутренней сферы — круг радиуса \(r\). Поскольку плоскость проходит через центр, эти два круга концентрические. Сечение тела между сферами этой плоскостью является кольцом, ограниченным этими двумя концентрическими окружностями. Площадь такого кольца находится как разность площадей большего и меньшего кругов. Площадь большего круга равна \(\pi R^2\), а площадь меньшего круга равна \(\pi r^2\). Следовательно, площадь сечения в этом случае равна \(\pi R^2 — \pi r^2\), что можно записать как \(\pi(R^2 — r^2)\).
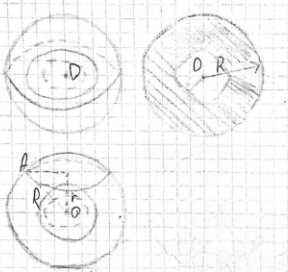
Теперь рассмотрим случай, когда секущая плоскость является касательной к внутренней сфере. Поскольку плоскость касается внутренней сферы, расстояние от центра сфер до этой плоскости равно радиусу внутренней сферы, то есть \(r\). Эта плоскость пересекает внешнюю сферу по окружности. Пусть \(x\) — радиус этой окружности сечения. Рассмотрим прямоугольный треугольник, вершинами которого являются общий центр сфер \(O\), точка касания плоскости к внутренней сфере \(T\), и любая точка \(P\) на окружности сечения внешней сферы. Отрезок \(OT\) перпендикулярен касательной плоскости и его длина равна \(r\). Отрезок \(OP\) является радиусом внешней сферы, поэтому его длина равна \(R\). Отрезок \(TP\) лежит в секущей плоскости и является радиусом окружности сечения, поэтому его длина равна \(x\). В прямоугольном треугольнике \(OTP\) с прямым углом при вершине \(T\) по теореме Пифагора имеем соотношение \(OT^2 + TP^2 = OP^2\), подставляя длины сторон получаем \(r^2 + x^2 = R^2\). Из этого уравнения найдем квадрат радиуса окружности сечения внешней сферы: \(x^2 = R^2 — r^2\). Сечение тела между сферами этой плоскостью является кругом радиуса \(x\). Площадь этого круга равна \(\pi x^2\). Подставляя найденное значение для \(x^2\), получаем, что площадь сечения в этом случае равна \(\pi(R^2 — r^2)\).
Сравнивая площади сечений в обоих случаях, мы видим, что площадь сечения плоскостью, проходящей через центр сфер \(\pi(R^2 — r^2)\), равна площади сечения плоскостью, касательной к внутренней сфере \(\pi(R^2 — r^2)\). Таким образом, утверждение задачи доказано.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.