Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 420 Атанасян — Подробные Ответы
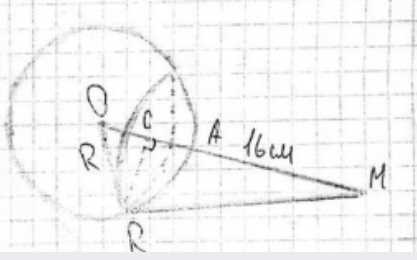
Вне сферы радиуса 10 см дана точка М на расстоянии 16 см от ближайшей точки сферы. Найдите длину такой окружности на сфере, все точки которой удалены от точки М на расстояние 24 см.
Пусть R — радиус сферы, R=10 см. Пусть А — ближайшая точка на сфере к точке М, лежащей вне сферы. Пусть С — центр окружности на сфере, все точки которой удалены от М на 24 см, и пусть r — радиус этой окружности. Тогда любая точка В на этой окружности удалена от М на 24 см, то есть ВМ=24 см. Точка С лежит на отрезке ОА, где О — центр сферы. Пусть АС = х. Тогда ОА = R = 10, ОС = ОА — АС = 10 — х.
Рассмотрим прямоугольный треугольник СВМ. По теореме Пифагора \(CM^2 + CB^2 = BM^2\). СМ = СА + АМ = х + 16. СВ = r. ВМ = 24. Получаем \((16+x)^2 + r^2 = 24^2 = 576\).
Рассмотрим прямоугольный треугольник СВО. По теореме Пифагора \(OC^2 + CB^2 = OB^2\). ОС = 10 — х. СВ = r. ОВ = R = 10. Получаем \((10-x)^2 + r^2 = 10^2 = 100\).
Решим систему уравнений:
\((16+x)^2 + r^2 = 576\)
\((10-x)^2 + r^2 = 100\)
Вычтем второе уравнение из первого:
\((16+x)^2 — (10-x)^2 = 576 — 100\)
\((256 + 32x + x^2) — (100 — 20x + x^2) = 476\)
\(256 + 32x + x^2 — 100 + 20x — x^2 = 476\)
\(156 + 52x = 476\)
\(52x = 476 — 156\)
\(52x = 320\)
\(x = \frac{320}{52} = \frac{80}{13}\) см.
Теперь найдем \(r^2\) из второго уравнения:
\(r^2 = 100 — (10-x)^2\)
Подставим значение х:
\(r^2 = 100 — \left(10 — \frac{80}{13}\right)^2 = 100 — \left(\frac{130 — 80}{13}\right)^2 = 100 — \left(\frac{50}{13}\right)^2\)
\(r^2 = 100 — \frac{2500}{169} = \frac{100 \times 169 — 2500}{169} = \frac{16900 — 2500}{169} = \frac{14400}{169}\)
\(r = \sqrt{\frac{14400}{169}} = \frac{120}{13}\) см.
Длина окружности на сфере вычисляется по формуле \(L = 2\pi r\).
\(L = 2\pi \left(\frac{120}{13}\right) = \frac{240\pi}{13}\) см.
Дано: сфера с центром О и радиусом R=10 см. Точка М находится вне сферы. Ближайшая точка на сфере к точке М — это точка А. Расстояние от А до М равно 16 см, то есть АМ = 16 см. На сфере есть окружность, все точки которой удалены от точки М на расстояние 24 см. Пусть В — любая точка на этой окружности, тогда ВМ = 24 см. Пусть С — центр этой окружности, а r — ее радиус, то есть СВ = r.
Поскольку А — ближайшая точка на сфере к М, точка А лежит на отрезке ОМ. Центр окружности С, лежащей на сфере, также лежит на отрезке ОА, который является частью радиуса сферы, перпендикулярного плоскости этой окружности. Пусть расстояние АС = х. Тогда расстояние от центра сферы О до центра окружности С равно ОС = ОА — АС = R — x = 10 — x.
Рассмотрим прямоугольный треугольник СВМ. Угол ВСМ = 90°, так как СВ — радиус окружности, а СМ лежит в плоскости, перпендикулярной радиусу в точке С. Расстояние СМ = СА + АМ = х + 16. По теореме Пифагора в треугольнике СВМ имеем: \(СМ^2 + СВ^2 = ВМ^2\). Подставляя известные значения, получаем \((16+x)^2 + r^2 = 24^2\), что равно \((16+x)^2 + r^2 = 576\).
Рассмотрим прямоугольный треугольник СВО. Угол ВСО = 90°, так как ОС перпендикулярно плоскости окружности, а СВ лежит в этой плоскости. Расстояние ОС = 10 — х. Расстояние СВ = r. Расстояние ОВ является радиусом сферы, ОВ = R = 10. По теореме Пифагора в треугольнике СВО имеем: \(ОС^2 + СВ^2 = ОВ^2\). Подставляя известные значения, получаем \((10-x)^2 + r^2 = 10^2\), что равно \((10-x)^2 + r^2 = 100\).
Мы получили систему из двух уравнений с двумя неизвестными х и r:
1) \((16+x)^2 + r^2 = 576\)
2) \((10-x)^2 + r^2 = 100\)
Вычтем второе уравнение из первого, чтобы исключить \(r^2\):
\((16+x)^2 — (10-x)^2 = 576 — 100\)
Раскроем квадраты:
\((256 + 32x + x^2) — (100 — 20x + x^2) = 476\)
\(256 + 32x + x^2 — 100 + 20x — x^2 = 476\)
Сгруппируем члены:
\((x^2 — x^2) + (32x + 20x) + (256 — 100) = 476\)
\(0 + 52x + 156 = 476\)
\(52x = 476 — 156\)
\(52x = 320\)
Найдем х:
\(x = \frac{320}{52} = \frac{160}{26} = \frac{80}{13}\) см.
Теперь подставим найденное значение х в любое из исходных уравнений, например, во второе, чтобы найти \(r^2\):
\((10-x)^2 + r^2 = 100\)
\(r^2 = 100 — (10-x)^2\)
Подставим \(x = \frac{80}{13}\):
\(r^2 = 100 — \left(10 — \frac{80}{13}\right)^2\)
Приведем к общему знаменателю в скобках:
\(10 — \frac{80}{13} = \frac{10 \times 13}{13} — \frac{80}{13} = \frac{130 — 80}{13} = \frac{50}{13}\)
Теперь подставим это значение обратно в выражение для \(r^2\):
\(r^2 = 100 — \left(\frac{50}{13}\right)^2 = 100 — \frac{50^2}{13^2} = 100 — \frac{2500}{169}\)
Приведем к общему знаменателю:
\(r^2 = \frac{100 \times 169}{169} — \frac{2500}{169} = \frac{16900 — 2500}{169} = \frac{14400}{169}\)
Найдем r, извлекая квадратный корень:
\(r = \sqrt{\frac{14400}{169}} = \frac{\sqrt{14400}}{\sqrt{169}} = \frac{120}{13}\) см.
Нас просят найти длину окружности. Длина окружности вычисляется по формуле \(L = 2\pi r\).
Подставим найденное значение r:
\(L = 2\pi \left(\frac{120}{13}\right) = \frac{2 \times 120 \times \pi}{13} = \frac{240\pi}{13}\) см.
Таким образом, длина окружности на сфере, все точки которой удалены от точки М на расстояние 24 см, равна \(\frac{240\pi}{13}\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.