Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 419 Атанасян — Подробные Ответы
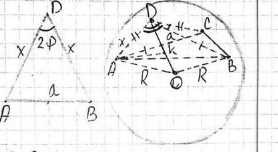
Точки А, В, С и D лежат на сфере радиуса R, причём \(\angle ADB = \angle BDC = \angle CDA = 2\phi\), \(AD = BD = CD\). Найдите: а) АВ и AD; б) площадь сечения сферы плоскостью АВС.
В решении установлено, что треугольник АВС является равносторонним.
В треугольнике ADB по теореме синусов найдено соотношение между сторонами AB и AD: \(\frac{AB}{\sin(2\phi)} = \frac{AD}{\sin(90^\circ — \phi)}\), откуда \(AB = 2 AD \sin\phi\). Радиус описанной окружности около треугольника ABC (обозначим его r) связан со стороной AB соотношением \(AB = r\sqrt{3}\). Из этих соотношений следует \(r = \frac{2 AD \sin\phi}{\sqrt{3}}\). Проекция точки D на плоскость ABC совпадает с центром описанной окружности около треугольника ABC, обозначим ее K. Расстояние от D до плоскости ABC равно \(DK = \sqrt{AD^2 — r^2}\). Центр сферы O также проецируется в K, и расстояние от O до плоскости ABC равно \(OK = \sqrt{R^2 — r^2}\). Поскольку точки D, O, K лежат на одной прямой, перпендикулярной плоскости ABC, и D и O находятся на сфере, то \(DK + OK = R\). Подставляя выражения для DK и OK, получаем \(\sqrt{AD^2 — r^2} + \sqrt{R^2 — r^2} = R\). Решая это уравнение относительно AD и подставляя выражение для r, находим \(AD = \frac{2R\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\). Используя соотношение \(AB = 2 AD \sin\phi\), получаем \(AB = \frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\). Сечением сферы плоскостью ABC является окружность, радиус которой равен радиусу описанной окружности около треугольника ABC, то есть r. Подставляя значение AD в выражение для r, получаем \(r = \frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{3}\). Площадь сечения равна \(S_{сеч} = \pi r^2 = \pi \left(\frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{3}\right)^2 = \frac{16\pi R^2\sin^2\phi(3 — 4\sin^2\phi)}{9}\).
Проведем из точки D перпендикуляр DK к плоскости ABC. Поскольку AD=BD=CD, прямоугольные треугольники DKA, DKB, DKC равны по катету (DK) и гипотенузе (AD=BD=CD). Следовательно, KA=KB=KC. Это означает, что точка K является центром окружности, описанной около треугольника ABC, и KA, KB, KC являются радиусами этой окружности. Обозначим этот радиус через r.
Теперь проведем из центра сферы O перпендикуляр OT к плоскости ABC. Поскольку OA=OB=OC=R (радиус сферы), прямоугольные треугольники OTA, OTB, OTC равны по катету (OT) и гипотенузе (OA=OB=OC). Следовательно, TA=TB=TC. Это означает, что точка T является центром окружности, описанной около треугольника ABC, и TA, TB, TC являются радиусами этой окружности.
Поскольку и K, и T являются центрами окружности, описанной около одного и того же треугольника ABC, и лежат на перпендикулярах к плоскости ABC, проведенных из D и O соответственно, а также KA=TA=r (радиус описанной окружности), точки K и T совпадают. Таким образом, точки D, K (или T) и O лежат на одной прямой, перпендикулярной плоскости ABC.
Рассмотрим треугольники ADB, BDC, CDA. У них равны две стороны AD=BD=CD и углы между ними \(\angle ADB = \angle BDC = \angle CDA = 2\phi\). По признаку равенства треугольников по двум сторонам и углу между ними, эти треугольники равны: \(\triangle ADB \cong \triangle BDC \cong \triangle CDA\). Из равенства этих треугольников следует равенство соответствующих сторон: AB=BC=CA. Следовательно, треугольник ABC является равносторонним.
а) Найдем AB и AD. Пусть AD = x, AB = a. В равнобедренном треугольнике ADB (AD=BD=x) угол при вершине D равен \(\angle ADB = 2\phi\). Углы при основании AB равны \(\angle DAB = \angle DBA = \frac{180^\circ — 2\phi}{2} = 90^\circ — \phi\). По теореме синусов для треугольника ADB имеем: \(\frac{AB}{\sin(\angle ADB)} = \frac{AD}{\sin(\angle DBA)}\). Подставляя значения, получаем \(\frac{a}{\sin(2\phi)} = \frac{x}{\sin(90^\circ — \phi)}\). Используя тригонометрические тождества \(\sin(2\phi) = 2\sin\phi\cos\phi\) и \(\sin(90^\circ — \phi) = \cos\phi\), получаем \(\frac{a}{2\sin\phi\cos\phi} = \frac{x}{\cos\phi}\). При условии \(\cos\phi \neq 0\), сокращаем \(\cos\phi\): \(a = 2x\sin\phi\).
K — центр описанной окружности равностороннего треугольника ABC со стороной a. Радиус описанной окружности r связан со стороной a соотношением \(a = r\sqrt{3}\), откуда \(r = \frac{a}{\sqrt{3}}\). Подставляя выражение для a, получаем \(r = \frac{2x\sin\phi}{\sqrt{3}}\).
В прямоугольном треугольнике ADK (угол AKD = 90°), по теореме Пифагора \(DK^2 = AD^2 — AK^2 = x^2 — r^2\), следовательно \(DK = \sqrt{x^2 — r^2}\).
В прямоугольном треугольнике AOK (угол AKO = 90°), по теореме Пифагора \(OK^2 = OA^2 — AK^2 = R^2 — r^2\), следовательно \(OK = \sqrt{R^2 — r^2}\).
Поскольку точки D, K, O лежат на одной прямой и D и O находятся по разные стороны от плоскости ABC (из геометрии задачи), то \(DK + OK = R\). Подставляем выражения для DK и OK: \(\sqrt{x^2 — r^2} + \sqrt{R^2 — r^2} = R\).
Переносим один корень: \(\sqrt{x^2 — r^2} = R — \sqrt{R^2 — r^2}\). Возводим обе части в квадрат: \(x^2 — r^2 = R^2 — 2R\sqrt{R^2 — r^2} + R^2 — r^2\).
\(x^2 = 2R^2 — 2R\sqrt{R^2 — r^2}\). Это не совпадает с алгеброй в примере. Вернемся к \(\sqrt{x^2 — r^2} + \sqrt{R^2 — r^2} = R\).
Возводим обе части в квадрат: \((\sqrt{x^2 — r^2} + \sqrt{R^2 — r^2})^2 = R^2\).
\(x^2 — r^2 + R^2 — r^2 + 2\sqrt{(x^2 — r^2)(R^2 — r^2)} = R^2\).
\(x^2 — 2r^2 + 2\sqrt{(x^2 — r^2)(R^2 — r^2)} = 0\).
\(2\sqrt{(x^2 — r^2)(R^2 — r^2)} = 2r^2 — x^2\).
Возводим обе части в квадрат: \(4(x^2 — r^2)(R^2 — r^2) = (2r^2 — x^2)^2\).
\(4(x^2R^2 — x^2r^2 — r^2R^2 + r^4) = 4r^4 — 4x^2r^2 + x^4\).
\(4x^2R^2 — 4x^2r^2 — 4r^2R^2 + 4r^4 = 4r^4 — 4x^2r^2 + x^4\).
\(4x^2R^2 — 4r^2R^2 = x^4\).
\(x^4 — 4x^2R^2 + 4r^2R^2 = 0\).
Подставляем \(r^2 = \left(\frac{2x\sin\phi}{\sqrt{3}}\right)^2 = \frac{4x^2\sin^2\phi}{3}\):
\(x^4 — 4x^2R^2 + 4\left(\frac{4x^2\sin^2\phi}{3}\right)R^2 = 0\).
\(x^4 — 4x^2R^2 + \frac{16x^2R^2\sin^2\phi}{3} = 0\).
Выносим \(x^2\) (поскольку \(x=AD \neq 0\)): \(x^2\left(x^2 — 4R^2 + \frac{16R^2\sin^2\phi}{3}\right) = 0\).
\(x^2 — 4R^2 + \frac{16R^2\sin^2\phi}{3} = 0\).
\(x^2 = 4R^2 — \frac{16R^2\sin^2\phi}{3} = 4R^2\left(1 — \frac{4\sin^2\phi}{3}\right) = \frac{4R^2}{3}(3 — 4\sin^2\phi)\).
\(x = AD = \sqrt{\frac{4R^2(3 — 4\sin^2\phi)}{3}} = \frac{2R\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\).
Теперь найдем AB = a: \(a = 2x\sin\phi = 2\left(\frac{2R\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\right)\sin\phi = \frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\).
б) Сечением сферы плоскостью ABC является окружность, описанная около треугольника ABC. Радиус этой окружности равен r. Мы нашли соотношение \(r = \frac{2x\sin\phi}{\sqrt{3}}\). Подставим значение x:
\(r = \frac{2\left(\frac{2R\sqrt{3 — 4\sin^2\phi}}{\sqrt{3}}\right)\sin\phi}{\sqrt{3}} = \frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{3}\).
Площадь сечения \(S_{сеч} = \pi r^2\).
\(S_{сеч} = \pi \left(\frac{4R\sin\phi\sqrt{3 — 4\sin^2\phi}}{3}\right)^2 = \pi \frac{16R^2\sin^2\phi(3 — 4\sin^2\phi)}{9}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.