Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 418 Атанасян — Подробные Ответы
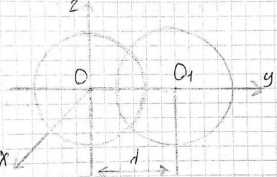
Расстояние между центрами двух равных сфер меньше их диаметра. а) Докажите, что пересечением этих сфер является окружность. б) Найдите радиус этой окружности, если радиусы сфер равны R, а расстояние между их центрами равно \(1,6R\).
Решение: Выберем систему координат. Уравнение сферы с центром в точке O: \(x^2+y^2+z^2=R^2\). Уравнение сферы с центром в точке O₁: \(x^2+(y-d)^2+z^2=R^2\).
Решение системы уравнений: \(\{x^2+y^2+z^2=R^2, x^2+(y-d)^2+z^2=R^2\}\) дает ответ на вопрос задачи. Вычитая второе уравнение из первого, получим \(y^2-(y-d)^2=0\), что упрощается до \(2yd-d^2=0\). Поскольку \(d>0\), имеем \(2y=d\), то есть \(y=\frac{d}{2}\). Это означает, что пересечение сфер лежит в плоскости \(y=\frac{d}{2}\), перпендикулярной оси ординат и параллельной плоскости Oxz. Подставим значение \(y=\frac{d}{2}\) в уравнение первой сферы: \(x^2+(\frac{d}{2})^2+z^2=R^2\). Отсюда \(x^2+z^2=R^2-(\frac{d}{2})^2\). Это уравнение окружности в плоскости \(y=\frac{d}{2}\) с радиусом \(r=\sqrt{R^2-(\frac{d}{2})^2}\). Утверждение а) доказано. Для части б) при \(d=1,6R\), радиус окружности равен \(r=\sqrt{R^2-(\frac{1,6R}{2})^2}=\sqrt{R^2-(0,8R)^2}=\sqrt{R^2-0,64R^2}=\)
\(=\sqrt{0,36R^2}=0,6R\).
Решение задачи состоит из двух частей: доказательства, что пересечение двух равных сфер, расстояние между центрами которых меньше их диаметра, является окружностью, и нахождения радиуса этой окружности при заданных условиях.
Для решения задачи выберем декартову систему координат. Пусть центр первой сферы O находится в начале координат \((0, 0, 0)\). Уравнение этой сферы с радиусом R будет \(x^2+y^2+z^2=R^2\).
Вторую сферу с таким же радиусом R расположим так, чтобы ее центр O₁ находился на оси ординат на расстоянии d от начала координат. Координаты центра O₁ будут \((0, d, 0)\). Уравнение второй сферы будет \(x^2+(y-d)^2+z^2=R^2\).
Пересечение этих двух сфер представляет собой множество точек \((x, y, z)\), которые удовлетворяют обоим уравнениям одновременно. Следовательно, для нахождения точек пересечения необходимо решить систему уравнений:
\(x^2+y^2+z^2=R^2\)
\(x^2+(y-d)^2+z^2=R^2\)
Вычтем второе уравнение из первого. Это позволит исключить члены \(x^2\) и \(z^2\), которые одинаковы в обоих уравнениях:
\((x^2+y^2+z^2) — (x^2+(y-d)^2+z^2) = R^2 — R^2\)
\(y^2 — (y-d)^2 = 0\)
Раскроем скобки во втором члене:
\(y^2 — (y^2 — 2yd + d^2) = 0\)
\(y^2 — y^2 + 2yd — d^2 = 0\)
\(2yd — d^2 = 0\)
Вынесем d за скобки:
\(d(2y — d) = 0\)
Это уравнение имеет два возможных решения: \(d=0\) или \(2y-d=0\). По условию задачи, расстояние между центрами d меньше диаметра \(2R\), что подразумевает \(d>0\). Следовательно, единственно возможное решение для y из этого уравнения при \(d>0\) есть:
\(2y — d = 0\)
\(2y = d\)
\(y = \frac{d}{2}\)
Это результат означает, что все точки пересечения обеих сфер лежат в плоскости, определяемой уравнением \(y=\frac{d}{2}\). Эта плоскость перпендикулярна оси ординат (оси y) и, следовательно, параллельна плоскости Oxz.
Теперь подставим значение \(y=\frac{d}{2}\) обратно в уравнение любой из сфер, например, в уравнение первой сферы \(x^2+y^2+z^2=R^2\):
\(x^2 + (\frac{d}{2})^2 + z^2 = R^2\)
\(x^2 + \frac{d^2}{4} + z^2 = R^2\)
Перегруппируем члены, чтобы выделить уравнение в плоскости \(y=\frac{d}{2}\):
\(x^2 + z^2 = R^2 — \frac{d^2}{4}\)
Это уравнение имеет вид \(x^2+z^2=r^2\), где \(r^2 = R^2 — \frac{d^2}{4}\). Это стандартное уравнение окружности в плоскости Oxz (или любой плоскости, параллельной Oxz, как в нашем случае плоскости \(y=\frac{d}{2}\)) с центром в точке \((0, \frac{d}{2}, 0)\) и радиусом \(r = \sqrt{R^2 — \frac{d^2}{4}}\).
По условию задачи, расстояние между центрами \(d < 2R\), что эквивалентно \(\frac{d}{2} < R\). Возводя обе части в квадрат, получаем \((\frac{d}{2})^2 < R^2\), или \(\frac{d^2}{4} < R^2\). Это гарантирует, что выражение под квадратным корнем \(R^2 - \frac{d^2}{4}\) является положительным, а значит, радиус r является действительным положительным числом, и пересечение действительно является окружностью. Таким образом, утверждение а) доказано. Для части б) задачи нам дано, что радиусы сфер равны R, а расстояние между их центрами равно \(d = 1,6R\). Нам нужно найти радиус окружности пересечения. Используем формулу для радиуса r, которую мы вывели в части а): \(r = \sqrt{R^2 - \frac{d^2}{4}}\) Подставим значение \(d = 1,6R\) в эту формулу: \(r = \sqrt{R^2 - \frac{(1,6R)^2}{4}}\) \(r = \sqrt{R^2 - \frac{2,56R^2}{4}}\) \(r = \sqrt{R^2 - 0,64R^2}\) Вычтем: \(r = \sqrt{(1 - 0,64)R^2}\) \(r = \sqrt{0,36R^2}\) Извлечем квадратный корень: \(r = 0,6R\) Таким образом, радиус окружности пересечения равен \(0,6R\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.