
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 417 Атанасян — Подробные Ответы
Два прямоугольника лежат в различных плоскостях и имеют общую сторону. Докажите, что все вершины данных прямоугольников лежат на одной сфере.
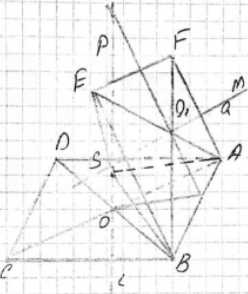
Пусть даны два прямоугольника ABCD и ABEF, лежащие в различных плоскостях и имеющие общую сторону AB. Пусть O — точка пересечения диагоналей прямоугольника ABCD, а O’ — точка пересечения диагоналей прямоугольника ABEF. Проведем прямую \(l\) через точку O перпендикулярно плоскости ABCD. Все точки прямой \(l\) равноудалены от вершин A, B, C, D прямоугольника ABCD, так как проекции отрезков, соединяющих точку на \(l\) с вершинами, равны (это половины диагоналей прямоугольника). Проведем прямую \(m\) через точку O’ перпендикулярно плоскости ABEF. Все точки прямой \(m\) равноудалены от вершин A, B, E, F прямоугольника ABEF.
Поскольку плоскости ABCD и ABEF различны и имеют общую прямую AB, они пересекаются по прямой AB. Прямая \(l\) перпендикулярна плоскости ABCD, а прямая \(m\) перпендикулярна плоскости ABEF. Прямая AB перпендикулярна любой прямой в плоскости ABCD, проходящей через точку O и перпендикулярной AB. Аналогично, прямая AB перпендикулярна любой прямой в плоскости ABEF, проходящей через точку O’ и перпендикулярной AB.
Прямые \(l\) и \(m\) пересекаются в некоторой точке S. Точка S лежит на прямой \(l\), поэтому она равноудалена от вершин A, B, C, D, то есть \(SA = SB = SC = SD\). Точка S также лежит на прямой \(m\), поэтому она равноудалена от вершин A, B, E, F, то есть \(SA = SB = SE = SF\).
Из равенств \(SA = SB = SC = SD\) и \(SA = SB = SE = SF\) следует, что \(SA = SB = SC = SD = SE = SF\). Таким образом, точка S равноудалена от всех вершин A, B, C, D, E, F данных прямоугольников. Следовательно, все эти вершины лежат на сфере с центром в точке S и радиусом, равным \(SA\).
Пусть даны два прямоугольника ABCD и ABEF, лежащие в различных плоскостях и имеющие общую сторону AB. Нам необходимо доказать, что все вершины этих двух прямоугольников лежат на одной сфере.
Рассмотрим сначала прямоугольник ABCD. Диагонали прямоугольника пересекаются в точке O, которая является их серединой. При этом диагонали прямоугольника равны, то есть \(AC = BD\), и делятся точкой пересечения пополам, так что \(OA = OB = OC = OD\). Рассмотрим прямую \(l\), проходящую через точку O перпендикулярно плоскости прямоугольника ABCD. Возьмем произвольную точку S на этой прямой \(l\). Соединим точку S с вершинами прямоугольника A, B, C, D. Получим отрезки SA, SB, SC, SD. Рассмотрим треугольники \(\triangle SOA\), \(\triangle SOB\), \(\triangle SOC\), \(\triangle SOD\). Поскольку прямая \(l\) перпендикулярна плоскости ABCD, отрезок SO перпендикулярен любой прямой в этой плоскости, проходящей через O. Следовательно, SO перпендикулярен OA, OB, OC, OD. Таким образом, треугольники \(\triangle SOA\), \(\triangle SOB\), \(\triangle SOC\), \(\triangle SOD\) являются прямоугольными с прямым углом при вершине O. В этих прямоугольных треугольниках отрезок SO является общим катетом. Отрезки OA, OB, OC, OD являются другими катетами, и, как мы установили, они равны: \(OA = OB = OC = OD\). По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов. Следовательно, \(SA^2 = SO^2 + OA^2\), \(SB^2 = SO^2 + OB^2\), \(SC^2 = SO^2 + OC^2\), \(SD^2 = SO^2 + OD^2\). Поскольку \(SO^2\) общий и \(OA^2 = OB^2 = OC^2 = OD^2\), получаем \(SA^2 = SB^2 = SC^2 = SD^2\). Извлекая квадратный корень, получаем \(SA = SB = SC = SD\). Это означает, что любая точка на прямой \(l\) равноудалена от всех вершин прямоугольника ABCD.
Теперь рассмотрим второй прямоугольник ABEF. Диагонали этого прямоугольника пересекаются в точке O’, которая является их серединой. Диагонали равны, \(AE = BF\), и делятся точкой пересечения пополам, так что \(O’A = O’B = O’E = O’F\). Рассмотрим прямую \(m\), проходящую через точку O’ перпендикулярно плоскости прямоугольника ABEF. Возьмем произвольную точку S’ на этой прямой \(m\). Соединим точку S’ с вершинами прямоугольника A, B, E, F. Получим отрезки S’A, S’B, S’E, S’F. Рассмотрим треугольники \(\triangle S’O’A\), \(\triangle S’O’B\), \(\triangle S’O’E\), \(\triangle S’O’F\). Поскольку прямая \(m\) перпендикулярна плоскости ABEF, отрезок S’O’ перпендикулярен любой прямой в этой плоскости, проходящей через O’. Следовательно, S’O’ перпендикулярен O’A, O’B, O’E, O’F. Таким образом, треугольники \(\triangle S’O’A\), \(\triangle S’O’B\), \(\triangle S’O’E\), \(\triangle S’O’F\) являются прямоугольными с прямым углом при вершине O’. В этих прямоугольных треугольниках отрезок S’O’ является общим катетом. Отрезки O’A, O’B, O’E, O’F являются другими катетами, и они равны: \(O’A = O’B = O’E = O’F\). По теореме Пифагора \(S’A^2 = S’O’^2 + O’A^2\), \(S’B^2 = S’O’^2 + O’B^2\), \(S’E^2 = S’O’^2 + O’E^2\), \(S’F^2 = S’O’^2 + O’F^2\). Поскольку \(S’O’^2\) общий и \(O’A^2 = O’B^2 = O’E^2 = O’F^2\), получаем \(S’A^2 = S’B^2 = S’E^2 = S’F^2\). Извлекая квадратный корень, получаем \(S’A = S’B = S’E = S’F\). Это означает, что любая точка на прямой \(m\) равноудалена от всех вершин прямоугольника ABEF.
Плоскости прямоугольников ABCD и ABEF различны, но имеют общую прямую AB. Прямая \(l\) перпендикулярна плоскости ABCD, а прямая \(m\) перпендикулярна плоскости ABEF. Поскольку плоскости различны, но пересекаются, перпендикуляры к этим плоскостям, проходящие через точки O и O’ соответственно, также должны пересекаться (если только они не параллельны, что возможно только если плоскости параллельны, а это не наш случай). Прямые \(l\) и \(m\) пересекаются в некоторой точке S.
Поскольку точка S лежит на прямой \(l\), она равноудалена от вершин A, B, C, D. Следовательно, \(SA = SB = SC = SD\).
Поскольку точка S лежит на прямой \(m\), она равноудалена от вершин A, B, E, F. Следовательно, \(SA = SB = SE = SF\).
Объединяя эти равенства, получаем \(SA = SB = SC = SD = SE = SF\).
Таким образом, точка S равноудалена от всех шести вершин A, B, C, D, E, F данных прямоугольников. По определению сферы, множество всех точек, равноудаленных от данной точки (центра сферы), лежит на сфере. Следовательно, все вершины A, B, C, D, E, F лежат на сфере с центром в точке S и радиусом, равным расстоянию от S до любой из этих вершин, например, \(R = SA\).
Таким образом, мы доказали, что все вершины данных прямоугольников лежат на одной сфере.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!