
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 416 Атанасян — Подробные Ответы
Точка А лежит на радиусе данной сферы с центром О и делит этот радиус в отношении 1 : 2, считая от центра сферы. Через точку А проведена плоскость \(\alpha\) так, что радиус сферы с центром О, касающейся плоскости \(\alpha\), в 6 раз меньше радиуса данной сферы. Найдите: а) угол между прямой ОА и плоскостью \(\alpha\); б) отношение площади сечения данной сферы плоскостью \(\alpha\) к площади самой сферы.
Пусть радиус данной сферы с центром О равен R. Согласно условию, точка А лежит на радиусе и делит его в отношении 1:2, считая от центра О. Это означает, что расстояние от центра О до точки А составляет одну треть радиуса сферы, то есть \(OA = \frac{1}{3}R\).
Через точку А проведена плоскость \(\alpha\). Эта плоскость касается меньшей сферы с центром О, радиус которой в 6 раз меньше радиуса данной сферы. Обозначим радиус меньшей сферы через r. Тогда \(r = \frac{1}{6}R\).
Плоскость \(\alpha\) является касательной к меньшей сфере с центром О. Пусть Р — точка касания меньшей сферы с плоскостью \(\alpha\). Радиус, проведенный в точку касания, перпендикулярен касательной плоскости, поэтому отрезок ОР перпендикулярен плоскости \(\alpha\), и его длина равна радиусу меньшей сферы: \(OP = r = \frac{1}{6}R\).
Теперь найдем угол между прямой ОА и плоскостью \(\alpha\). Углом между прямой и плоскостью является угол между прямой и ее проекцией на эту плоскость. Рассмотрим прямоугольный треугольник ОРА, где угол ОРА прямой, так как ОР перпендикулярен плоскости \(\alpha\), а значит, и любой прямой, лежащей в этой плоскости и проходящей через Р, в частности, прямой АР, которая является проекцией ОА на плоскость \(\alpha\). Гипотенузой в этом треугольнике является отрезок ОА. Угол между прямой ОА и плоскостью \(\alpha\) — это угол между ОА и АР, то есть угол \(\angle OAP\).
В прямоугольном треугольнике ОРА синус угла \(\angle OAP\) равен отношению длины противолежащего катета ОР к длине гипотенузы ОА.
Таким образом, \(\sin(\angle OAP) = \frac{OP}{OA}\).
Подставляя известные значения \(OP = \frac{1}{6}R\) и \(OA = \frac{1}{3}R\), получаем:
\(\sin(\angle OAP) = \frac{\frac{1}{6}R}{\frac{1}{3}R} = \frac{1}{6}R \times \frac{3}{1}R = \frac{3}{6} = \frac{1}{2}\).
Поскольку \(\sin(\angle OAP) = \frac{1}{2}\), угол \(\angle OAP\) равен \(30^\circ\).
Этот угол и является углом между прямой ОА и плоскостью \(\alpha\).
Далее найдем отношение площади сечения данной сферы плоскостью \(\alpha\) к площади самой сферы.
Сечением сферы плоскостью является окружность. Центр этой окружности — это проекция центра сферы О на плоскость \(\alpha\), то есть точка Р. Радиус сечения — это расстояние от точки Р до любой точки на линии пересечения сферы и плоскости. Пусть Т — произвольная точка на линии пересечения. Тогда Т лежит на сфере, и отрезок ОТ является радиусом данной сферы, \(OT = R\). Отрезок РТ является радиусом окружности сечения. Треугольник ОРТ является прямоугольным с прямым углом при вершине Р, поскольку ОР перпендикулярен плоскости сечения, в которой лежит отрезок РТ.
По теореме Пифагора в прямоугольном треугольнике ОРТ имеем: \(OT^2 = OP^2 + PT^2\).
Из этого равенства выразим квадрат радиуса сечения \(PT^2\):
\(PT^2 = OT^2 — OP^2\).
Мы знаем, что \(OT = R\) и \(OP = \frac{1}{6}R\). Подставляем эти значения:
\(PT^2 = R^2 — \left(\frac{1}{6}R\right)^2 = R^2 — \frac{1}{36}R^2 = \frac{36R^2 — 1R^2}{36} = \frac{35R^2}{36}\).
Площадь окружности сечения \(S_{сечения}\) вычисляется по формуле \(S = \pi r_{сечения}^2\), где \(r_{сечения} = PT\).
\(S_{сечения} = \pi (PT)^2 = \pi \frac{35R^2}{36}\).
Площадь поверхности данной сферы \(S_{сферы}\) вычисляется по формуле \(S = 4\pi R^2\).
\(S_{сферы} = 4\pi R^2\).
Теперь найдем отношение площади сечения к площади сферы:
\(\frac{S_{сечения}}{S_{сферы}} = \frac{\pi \frac{35R^2}{36}}{4\pi R^2}\).
Сократим \(\pi\) и \(R^2\) (при условии \(R \neq 0\)):
\(\frac{S_{сечения}}{S_{сферы}} = \frac{\frac{35}{36}}{4} = \frac{35}{36 \times 4} = \frac{35}{144}\).
Таким образом, отношение площади сечения данной сферы плоскостью \(\alpha\) к площади самой сферы равно \(\frac{35}{144}\).
Решение: Пусть радиус данной сферы с центром О равен \(3х\). По условию, точка А лежит на радиусе так, что расстояние от центра О до точки А равно \(х\), то есть \(OA = x\). Через точку А проведена плоскость \(\alpha\). Эта плоскость касается меньшей сферы с центром О, радиус которой равен \(\frac{1}{6}\) радиуса данной сферы. Радиус меньшей сферы \(r = \frac{1}{6}(3х) = \frac{x}{2}\). Пусть Р — точка касания меньшей сферы с плоскостью \(\alpha\). Отрезок ОР перпендикулярен плоскости \(\alpha\), и его длина равна радиусу меньшей сферы, то есть \(OP = \frac{x}{2}\).
а) Найдем угол между прямой ОА и плоскостью \(\alpha\). Углом между прямой и плоскостью является угол между прямой и ее проекцией на эту плоскость. Рассмотрим прямоугольный треугольник ОРА, где угол ОРА прямой, так как ОР перпендикулярен плоскости \(\alpha\). Гипотенузой в этом треугольнике является отрезок ОА. Угол между прямой ОА и плоскостью \(\alpha\) — это угол между ОА и АР, то есть угол \(\angle OAP\). В прямоугольном треугольнике ОРА синус угла \(\angle OAP\) равен отношению длины противолежащего катета ОР к длине гипотенузы ОА. \(\sin(\angle OAP) = \frac{OP}{OA}\). Подставляя значения \(OP = \frac{x}{2}\) и \(OA = x\), получаем \(\sin(\angle OAP) = \frac{x/2}{x} = \frac{1}{2}\). Поскольку \(\sin(\angle OAP) = \frac{1}{2}\), угол \(\angle OAP\) равен \(30^\circ\). Это и будет углом между прямой ОА и плоскостью \(\alpha\).
б) Найдем отношение площади сечения данной сферы плоскостью \(\alpha\) к площади самой сферы. Сечением сферы плоскостью является окружность. Центр этой окружности — это проекция центра сферы О на плоскость \(\alpha\), то есть точка Р. Радиус сечения — это расстояние от точки Р до любой точки на линии пересечения сферы и плоскости. Пусть Т — произвольная точка на линии пересечения. Тогда Т лежит на сфере, и отрезок ОТ является радиусом данной сферы, \(OT = 3x\). Отрезок РТ является радиусом окружности сечения. Треугольник ОРТ является прямоугольным с прямым углом при вершине Р, поскольку ОР перпендикулярен плоскости сечения, в которой лежит отрезок РТ. По теореме Пифагора в прямоугольном треугольнике ОРТ имеем: \(OT^2 = OP^2 + PT^2\). Отсюда выразим квадрат радиуса сечения \(PT^2\): \(PT^2 = OT^2 — OP^2\). Подставим известные значения \(OT = 3x\) и \(OP = \frac{x}{2}\). \(PT^2 = (3x)^2 — (\frac{x}{2})^2 = 9x^2 — \frac{x^2}{4} = \frac{36x^2 — x^2}{4} = \frac{35x^2}{4}\). Площадь окружности сечения \(S_{сечения}\) вычисляется по формуле \(S = \pi r_{сечения}^2\), где \(r_{сечения} = PT\). \(S_{сечения} = \pi (PT)^2 = \pi \frac{35x^2}{4}\). Площадь поверхности данной сферы \(S_{сферы}\) вычисляется по формуле \(S = 4\pi R^2\). \(S_{сферы} = 4\pi (3x)^2 = 4\pi (9x^2) = 36\pi x^2\). Теперь найдем отношение площади сечения к площади сферы: \(\frac{S_{сечения}}{S_{сферы}} = \frac{\pi \frac{35x^2}{4}}{36\pi x^2}\). Сократим \(\pi\) и \(x^2\) (при условии \(x \neq 0\)): \(\frac{S_{сечения}}{S_{сферы}} = \frac{35/4}{36} = \frac{35}{4 \times 36} = \frac{35}{144}\). Таким образом, отношение площади сечения данной сферы плоскостью \(\alpha\) к площади самой сферы равно \(\frac{35}{144}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


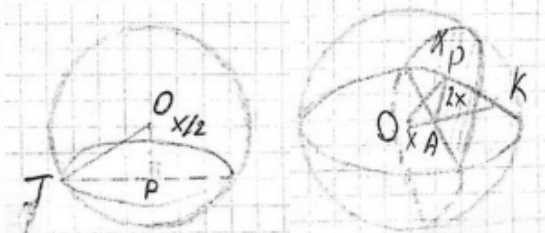

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!