Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 415 Атанасян — Подробные Ответы
Вершины прямоугольного треугольника с катетами 1,8 см и 2,4 см лежат на сфере. а) Докажите, что если радиус сферы равен 1,5 см, то центр сферы лежит в плоскости треугольника. б) Найдите расстояние от центра сферы до плоскости треугольника, если радиус сферы равен 6,5 см.
Решение:
а) Найдем длину гипотенузы прямоугольного треугольника: \(\sqrt{1.8^2 + 2.4^2} = \sqrt{3.24 + 5.76} = \sqrt{9} = 3\) см. Диаметр сферы равен \(2 \times 1.5 = 3\) см. Диаметр сферы совпадает с гипотенузой, значит, центр сферы находится на середине гипотенузы, т.е лежит в плоскости треугольника.
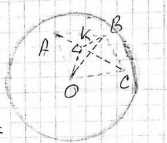
б) Плоскость ABC пересекает сферу по окружности, центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы. Проведем из точки O отрезок OK, перпендикулярный плоскости ABC. Отрезки OA, OB, OC равные наклонные имеют равные проекции на плоскость ABC, тогда KA=KB=KC, точка K равноудалена от вершин треугольника ABC, т.е она — центр описанной окружности. Таким образом, точка K — середина гипотенузы AC. OK — искомое расстояние. \(AC = 3\) см, \(AK = 1.5\) см. Из треугольника OKA по теореме Пифагора: \(OK = \sqrt{OA^2 — AK^2} = \sqrt{6.5^2 — 1.5^2} = \sqrt{42.25 — 2.25} = \sqrt{40} = 2\sqrt{10}\) см.
Решение:
а) Сначала найдем длину гипотенузы прямоугольного треугольника, используя теорему Пифагора. Катеты равны 1,8 см и 2,4 см. Длина гипотенузы \(c\) вычисляется как \(c = \sqrt{a^2 + b^2}\), где \(a\) и \(b\) — длины катетов. Подставляя значения, получаем \(c = \sqrt{1.8^2 + 2.4^2} = \sqrt{3.24 + 5.76} = \sqrt{9} = 3\) см.
Радиус сферы равен 1,5 см, следовательно, диаметр сферы равен \(2 \times 1.5 = 3\) см.
Мы видим, что диаметр сферы равен длине гипотенузы треугольника. Если все вершины треугольника лежат на сфере, и диаметр сферы равен длине одной из сторон треугольника, то эта сторона является диаметром окружности, по которой плоскость треугольника пересекает сферу. В случае прямоугольного треугольника, описанная окружность имеет своим диаметром гипотенузу, а ее центр лежит на середине гипотенузы. Поскольку диаметр сферы совпадает с гипотенузой, центр сферы совпадает с центром описанной окружности треугольника, который находится на середине гипотенузы. Таким образом, центр сферы лежит в плоскости треугольника.
б) Плоскость треугольника ABC пересекает сферу по окружности, которая является описанной окружностью этого прямоугольного треугольника. Центр этой описанной окружности (обозначим его K) лежит на середине гипотенузы AC.
Радиус сферы теперь равен 6,5 см. Точка K — середина гипотенузы AC. Длина гипотенузы AC, как мы нашли в пункте а), равна 3 см. Следовательно, расстояние от вершины A до середины гипотенузы K равно \(AK = AC / 2 = 3 / 2 = 1.5\) см.
Расстояние от центра сферы O до плоскости треугольника — это длина перпендикуляра OK, опущенного из центра сферы на плоскость треугольника. Точки A, B, и C лежат на сфере, поэтому расстояния от центра сферы до этих точек равны радиусу сферы: \(OA = OB = OC = 6.5\) см.
Отрезки OA, OB, OC являются наклонными к плоскости треугольника, а их проекциями на эту плоскость являются отрезки KA, KB, KC соответственно. Поскольку наклонные OA, OB, OC равны, их проекции KA, KB, KC также равны. Это подтверждает, что K является центром описанной окружности треугольника ABC, так как K равноудалена от вершин A, B, C.
В прямоугольном треугольнике OKA (где OK перпендикулярно плоскости ABC, а значит, и отрезку AK, лежащему в этой плоскости) мы можем использовать теорему Пифагора для нахождения длины OK. Гипотенуза этого треугольника — OA (радиус сферы), один катет — AK (половина гипотенузы треугольника ABC), а второй катет — OK (искомое расстояние).
По теореме Пифагора: \(OA^2 = OK^2 + AK^2\).
Отсюда выразим OK: \(OK^2 = OA^2 — AK^2\).
Подставим известные значения: \(OA = 6.5\) см и \(AK = 1.5\) см.
\(OK^2 = 6.5^2 — 1.5^2 = 42.25 — 2.25 = 40\).
Следовательно, \(OK = \sqrt{40}\). Упростим корень: \(40 = 4 \times 10\), поэтому \(\sqrt{40} = \sqrt{4 \times 10} = \sqrt{4} \times \sqrt{10} = 2\sqrt{10}\) см.
Таким образом, расстояние от центра сферы до плоскости треугольника равно \(2\sqrt{10}\) см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.