
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 412 Атанасян — Подробные Ответы
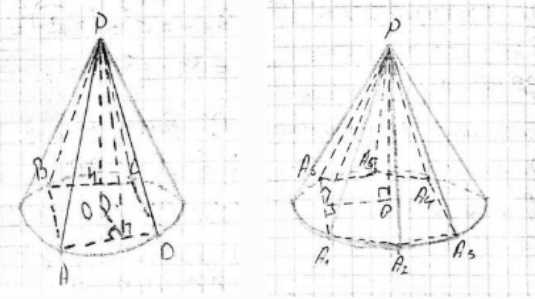
Высота конуса равна 4 см, а радиус основания равен 3 см. Вычислите площадь полной поверхности правильной n-угольной пирамиды, вписанной в конус, если: а) \(n = 3\); б) \(n = 4\); в) \(n = 6\).
Дано: высота конуса \(h = 4\) см, радиус основания конуса \(R = 3\) см.
Требуется найти площадь полной поверхности правильной n-угольной пирамиды, вписанной в конус, для случаев \(n=3\), \(n=4\), \(n=6\).
а) Случай \(n = 3\) (правильный треугольник в основании).
Сторона правильного треугольника, вписанного в окружность радиуса \(R\), равна \(a = 2R \sin(60^\circ) = 2 \cdot 3 \cdot \frac{\sqrt{3}}{2} = 3\sqrt{3}\) см.
Апофема правильного треугольника (радиус вписанной окружности) равна \(r_{in} = R \cos(60^\circ) = 3 \cdot \frac{1}{2} = 1.5 = \frac{3}{2}\) см.
Высота боковой грани пирамиды (апофема пирамиды) равна \(h_s = \sqrt{h^2 + r_{in}^2} = \sqrt{4^2 + (\frac{3}{2})^2} = \sqrt{16 + \frac{9}{4}} = \sqrt{\frac{64+9}{4}} = \sqrt{\frac{73}{4}} = \frac{\sqrt{73}}{2}\) см.
Площадь основания (правильного треугольника) равна \(S_{base} = \frac{\sqrt{3}}{4} a^2 = \frac{\sqrt{3}}{4} (3\sqrt{3})^2 = \frac{\sqrt{3}}{4} \cdot 27 = \frac{27\sqrt{3}}{4}\) см\(^2\).
Площадь боковой поверхности пирамиды равна \(S_{lateral} = 3 \cdot \frac{1}{2} a h_s = \frac{3}{2} (3\sqrt{3}) (\frac{\sqrt{73}}{2}) = \frac{9\sqrt{219}}{4}\) см\(^2\).
Площадь полной поверхности пирамиды равна \(S_{total} = S_{base} + S_{lateral} = \frac{27\sqrt{3}}{4} + \frac{9\sqrt{219}}{4} = \frac{9\sqrt{3}(3 + \sqrt{73})}{4}\) см\(^2\).
б) Случай \(n = 4\) (квадрат в основании).
Сторона квадрата, вписанного в окружность радиуса \(R\), равна \(a = R\sqrt{2} = 3\sqrt{2}\) см.
Апофема квадрата (половина стороны) равна \(r_{in} = \frac{a}{2} = \frac{3\sqrt{2}}{2}\) см.
Высота боковой грани пирамиды равна \(h_s = \sqrt{h^2 + r_{in}^2} = \sqrt{4^2 + (\frac{3\sqrt{2}}{2})^2} = \sqrt{16 + \frac{18}{4}} = \sqrt{16 + \frac{9}{2}} = \sqrt{\frac{32+9}{2}} =\)
\( =\sqrt{\frac{41}{2}}\) см.
Площадь основания (квадрата) равна \(S_{base} = a^2 = (3\sqrt{2})^2 = 18\) см\(^2\).
Площадь боковой поверхности пирамиды равна \(S_{lateral} = 4 \cdot \frac{1}{2} a h_s = 2 a h_s = 2 (3\sqrt{2}) (\sqrt{\frac{41}{2}}) = 6\sqrt{2} \frac{\sqrt{41}}{\sqrt{2}} = 6\sqrt{41}\) см\(^2\).
Площадь полной поверхности пирамиды равна \(S_{total} = S_{base} + S_{lateral} = 18 + 6\sqrt{41} = 6(3 + \sqrt{41})\) см\(^2\).
в) Случай \(n = 6\) (правильный шестиугольник в основании).
Сторона правильного шестиугольника, вписанного в окружность радиуса \(R\), равна \(a = R = 3\) см.
Апофема правильного шестиугольника равна \(r_{in} = R \cos(30^\circ) = 3 \cdot \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{2}\) см.
Высота боковой грани пирамиды равна \(h_s = \sqrt{h^2 + r_{in}^2} = \sqrt{4^2 + (\frac{3\sqrt{3}}{2})^2} = \sqrt{16 + \frac{27}{4}} = \sqrt{\frac{64+27}{4}} = \sqrt{\frac{91}{4}} =\)
\(= \frac{\sqrt{91}}{2}\) см.
Площадь основания (правильного шестиугольника) равна \(S_{base} = \frac{3\sqrt{3}}{2} a^2 = \frac{3\sqrt{3}}{2} (3)^2 = \frac{27\sqrt{3}}{2}\) см\(^2\).
Площадь боковой поверхности пирамиды равна \(S_{lateral} = 6 \cdot \frac{1}{2} a h_s = 3 a h_s = 3 \cdot 3 \cdot \frac{\sqrt{91}}{2} = \frac{9\sqrt{91}}{2}\) см\(^2\).
Площадь полной поверхности пирамиды равна \(S_{total} = S_{base} + S_{lateral} = \frac{27\sqrt{3}}{2} + \frac{9\sqrt{91}}{2} = \frac{9(3\sqrt{3} + \sqrt{91})}{2}\) см\(^2\).
Дано: высота конуса \(h = 4\) см, радиус основания конуса \(R = 3\) см.
Рассматривается правильная n-угольная пирамида, вписанная в данный конус. Это означает, что вершина пирамиды совпадает с вершиной конуса, а основание пирамиды вписано в основание конуса. Высота пирамиды равна высоте конуса, то есть \(h_{пир} = h = 4\) см. Радиус окружности, описанной вокруг основания пирамиды, равен радиусу основания конуса, то есть \(R_{осн} = R = 3\) см.
Площадь полной поверхности пирамиды \(S_{полн}\) складывается из площади основания \(S_{осн}\) и площади боковой поверхности \(S_{бок}\), то есть \(S_{полн} = S_{осн} + S_{бок}\). Основание пирамиды — правильный n-угольник, вписанный в окружность радиуса \(R = 3\) см. Боковые грани пирамиды — равные равнобедренные треугольники.
Для вычисления площади боковой поверхности нам понадобится апофема пирамиды (высота боковой грани). Апофему пирамиды \(h_a\) можно найти, зная высоту пирамиды \(h\) и радиус окружности, вписанной в основание пирамиды \(r_{впис}\). Треугольник, образованный высотой пирамиды, радиусом вписанной окружности основания и апофемой пирамиды, является прямоугольным, причем апофема пирамиды является гипотенузой. По теореме Пифагора \(h_a = \sqrt{h^2 + r_{впис}^2}\).
Радиус окружности, вписанной в правильный n-угольник со стороной \(a\), выражается формулой \(r_{впис} = \frac{a}{2 \tan(\frac{180^\circ}{n})}\). Сторона правильного n-угольника, вписанного в окружность радиуса \(R\), выражается формулой \(a = 2R \sin(\frac{180^\circ}{n})\). Подставив \(R=3\), получим \(a = 6 \sin(\frac{180^\circ}{n})\). Тогда \(r_{впис} = \frac{6 \sin(\frac{180^\circ}{n})}{2 \tan(\frac{180^\circ}{n})} = 3 \frac{\sin(\frac{180^\circ}{n})}{\frac{\sin(\frac{180^\circ}{n})}{\cos(\frac{180^\circ}{n})}} = 3 \cos(\frac{180^\circ}{n})\).
Площадь основания правильной n-угольной пирамиды можно найти как \(S_{осн} = \frac{1}{2} \cdot \text{периметр} \cdot r_{впис} = \frac{1}{2} \cdot (n \cdot a) \cdot r_{впис}\).
Площадь боковой поверхности пирамиды равна сумме площадей n боковых граней. Площадь одной боковой грани (равнобедренного треугольника) равна \(S_{грани} = \frac{1}{2} \cdot \text{основание} \cdot \text{высота} = \frac{1}{2} \cdot a \cdot h_a\). Тогда \(S_{бок} = n \cdot S_{грани} = n \cdot \frac{1}{2} a h_a\).
Рассмотрим случай а) \(n = 3\) (правильный треугольник в основании).
Сторона основания \(a = 6 \sin(\frac{180^\circ}{3}) = 6 \sin(60^\circ) = 6 \cdot \frac{\sqrt{3}}{2} = 3\sqrt{3}\) см.
Радиус вписанной окружности основания \(r_{впис} = 3 \cos(\frac{180^\circ}{3}) = 3 \cos(60^\circ) = 3 \cdot \frac{1}{2} = \frac{3}{2}\) см.
Апофема пирамиды \(h_a = \sqrt{h^2 + r_{впис}^2} = \sqrt{4^2 + (\frac{3}{2})^2} = \sqrt{16 + \frac{9}{4}} = \sqrt{\frac{64+9}{4}} = \sqrt{\frac{73}{4}} = \frac{\sqrt{73}}{2}\) см.
Площадь основания \(S_{осн} = \frac{1}{2} \cdot 3 \cdot a \cdot r_{впис} = \frac{3}{2} \cdot (3\sqrt{3}) \cdot (\frac{3}{2}) = \frac{27\sqrt{3}}{4}\) см\(^2\). Или по формуле площади правильного треугольника \(S_{осн} = \frac{\sqrt{3}}{4} a^2 = \frac{\sqrt{3}}{4} (3\sqrt{3})^2 = \frac{\sqrt{3}}{4} \cdot 27 = \frac{27\sqrt{3}}{4}\) см\(^2\).
Площадь боковой поверхности \(S_{бок} = 3 \cdot \frac{1}{2} a h_a = \frac{3}{2} (3\sqrt{3}) (\frac{\sqrt{73}}{2}) = \frac{9\sqrt{219}}{4}\) см\(^2\).
Площадь полной поверхности \(S_{полн} = S_{осн} + S_{бок} = \frac{27\sqrt{3}}{4} + \frac{9\sqrt{219}}{4} = \frac{9\sqrt{3}(3 + \sqrt{73})}{4}\) см\(^2\).
Рассмотрим случай б) \(n = 4\) (квадрат в основании).
Сторона основания \(a = 6 \sin(\frac{180^\circ}{4}) = 6 \sin(45^\circ) = 6 \cdot \frac{\sqrt{2}}{2} = 3\sqrt{2}\) см.
Радиус вписанной окружности основания \(r_{впис} = 3 \cos(\frac{180^\circ}{4}) = 3 \cos(45^\circ) = 3 \cdot \frac{\sqrt{2}}{2} = \frac{3\sqrt{2}}{2}\) см.
Апофема пирамиды \(h_a = \sqrt{h^2 + r_{впис}^2} = \sqrt{4^2 + (\frac{3\sqrt{2}}{2})^2} = \sqrt{16 + \frac{18}{4}} = \sqrt{16 + \frac{9}{2}} = \sqrt{\frac{32+9}{2}} =\)
\(= \sqrt{\frac{41}{2}}\) см.
Площадь основания \(S_{осн} = a^2 = (3\sqrt{2})^2 = 18\) см\(^2\).
Площадь боковой поверхности \(S_{бок} = 4 \cdot \frac{1}{2} a h_a = 2 a h_a = 2 (3\sqrt{2}) \sqrt{\frac{41}{2}} = 6\sqrt{2} \frac{\sqrt{41}}{\sqrt{2}} = 6\sqrt{41}\) см\(^2\).
Площадь полной поверхности \(S_{полн} = S_{осн} + S_{бок} = 18 + 6\sqrt{41} = 6(3 + \sqrt{41})\) см\(^2\).
Рассмотрим случай в) \(n = 6\) (правильный шестиугольник в основании).
Сторона основания \(a = 6 \sin(\frac{180^\circ}{6}) = 6 \sin(30^\circ) = 6 \cdot \frac{1}{2} = 3\) см.
Радиус вписанной окружности основания \(r_{впис} = 3 \cos(\frac{180^\circ}{6}) = 3 \cos(30^\circ) = 3 \cdot \frac{\sqrt{3}}{2} = \frac{3\sqrt{3}}{2}\) см.
Апофема пирамиды \(h_a = \sqrt{h^2 + r_{впис}^2} = \sqrt{4^2 + (\frac{3\sqrt{3}}{2})^2} = \sqrt{16 + \frac{27}{4}} = \sqrt{\frac{64+27}{4}} = \sqrt{\frac{91}{4}} =\)
\( =\frac{\sqrt{91}}{2}\) см.
Площадь основания \(S_{осн} = \frac{3\sqrt{3}}{2} a^2 = \frac{3\sqrt{3}}{2} (3)^2 = \frac{27\sqrt{3}}{2}\) см\(^2\).
Площадь боковой поверхности \(S_{бок} = 6 \cdot \frac{1}{2} a h_a = 3 a h_a = 3 \cdot 3 \cdot \frac{\sqrt{91}}{2} = \frac{9\sqrt{91}}{2}\) см\(^2\).
Площадь полной поверхности \(S_{полн} = S_{осн} + S_{бок} = \frac{27\sqrt{3}}{2} + \frac{9\sqrt{91}}{2} = \frac{9(3\sqrt{3} + \sqrt{91})}{2}\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!