
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 411 Атанасян — Подробные Ответы
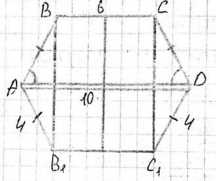
Равнобедренная трапеция, основания которой равны 6 см и 10 см, а острый угол \(60^\circ\), вращается вокруг большего основания. Вычислите площадь поверхности полученного тела
Тело вращения состоит из цилиндра и двух одинаковых конусов.
Проекция боковой стороны на большее основание трапеции равна \((10 — 6) / 2 = 2\) см. Высота трапеции \(h\), являющаяся радиусом \(r\) оснований цилиндра и конусов, равна \(2 \cdot \tan(60^\circ) = 2\sqrt{3}\) см. Боковая сторона трапеции \(l\), являющаяся образующей конусов, равна \(2 / \cos(60^\circ) = 4\) см. Высота цилиндра \(H_{цил}\) равна меньшему основанию трапеции, то есть \(6\) см. Площадь боковой поверхности цилиндра \(S_{цил} = 2\pi r H_{цил} = 2\pi \cdot 2\sqrt{3} \cdot 6 = 24\sqrt{3}\pi\) см\(^2\). Площадь боковой поверхности одного конуса \(S_{кон} = \pi r l = \pi \cdot 2\sqrt{3} \cdot 4 = 8\sqrt{3}\pi\) см\(^2\). Площадь поверхности тела вращения \(S = S_{цил} + 2 \cdot S_{кон} = 24\sqrt{3}\pi + 2 \cdot 8\sqrt{3}\pi = 24\sqrt{3}\pi + 16\sqrt{3}\pi = \)
\(=40\sqrt{3}\pi\) см\(^2\).
При вращении равнобедренной трапеции вокруг большего основания образуется тело, состоящее из центрального прямого кругового цилиндра и двух одинаковых прямых круговых конусов, примыкающих к его основаниям. Радиусы оснований цилиндра и конусов равны высоте трапеции, а высота цилиндра равна меньшему основанию трапеции. Образующая конусов равна боковой стороне трапеции.
Сначала найдем длину отрезка на большем основании трапеции, который является проекцией боковой стороны. Этот отрезок равен полуразности оснований: \((10 — 6) / 2 = 4 / 2 = 2\) см.
Теперь найдем высоту трапеции \(h\). В прямоугольном треугольнике, образованном боковой стороной, высотой и найденным отрезком, острый угол равен \(60^\circ\). Используя определение тангенса, получаем \(h = 2 \cdot \tan(60^\circ) = 2\sqrt{3}\) см. Эта высота является радиусом \(r\) оснований цилиндра и конусов, то есть \(r = 2\sqrt{3}\) см.
Далее найдем длину боковой стороны трапеции \(l\), которая является образующей конусов. Используя определение косинуса в том же прямоугольном треугольнике, получаем \(l = 2 / \cos(60^\circ) = 2 / (1/2) = 4\) см. Таким образом, образующая конусов равна \(l = 4\) см.
Высота цилиндра \(H_{цил}\) равна длине меньшего основания трапеции, то есть \(H_{цил} = 6\) см.
Площадь боковой поверхности цилиндра вычисляется по формуле \(S_{цил} = 2\pi r H_{цил}\). Подставляя найденные значения, получаем \(S_{цил} = 2\pi \cdot (2\sqrt{3}) \cdot 6 = 24\sqrt{3}\pi\) см\(^2\).
Площадь боковой поверхности одного конуса вычисляется по формуле \(S_{кон} = \pi r l\). Подставляя найденные значения, получаем \(S_{кон} = \pi \cdot (2\sqrt{3}) \cdot 4 = 8\sqrt{3}\pi\) см\(^2\).
Поскольку тело вращения имеет два одинаковых конуса, их общая боковая поверхность равна \(2 \cdot S_{кон} = 2 \cdot 8\sqrt{3}\pi = 16\sqrt{3}\pi\) см\(^2\).
Полная площадь поверхности тела вращения равна сумме площади боковой поверхности цилиндра и площадей боковых поверхностей двух конусов: \(S = S_{цил} + 2 \cdot S_{кон}\). Подставляя найденные значения, получаем \(S = 24\sqrt{3}\pi + 16\sqrt{3}\pi = 40\sqrt{3}\pi\) см\(^2\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!