ГДЗ по Геометрии 10 класс Номер 410 Атанасян — Подробные Ответы

Прямоугольный треугольник с катетами a и b вращается вокруг гипотенузы. Найдите площадь поверхности полученного тела.

Решение:

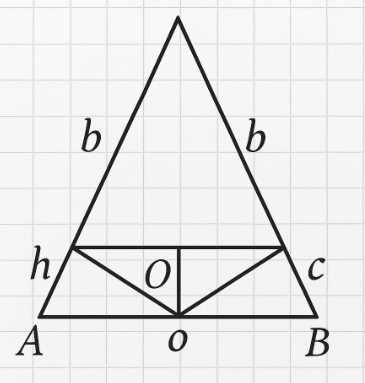
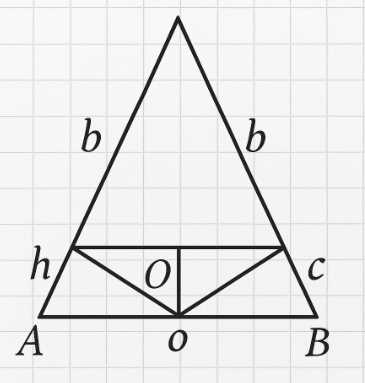
При вращении прямоугольного треугольника вокруг гипотенузы получим два конуса с общим основанием. Радиус этого основания равен высоте, опущенной из вершины прямого угла на гипотенузу.
Радиус основания \( r = \frac{ab}{\sqrt{a^2 + b^2}} \).
Боковая поверхность первого конуса с образующей \( a \) равна \( S_{бок1} = \pi r a = \pi \frac{ab}{\sqrt{a^2 + b^2}} a = \frac{\pi a^2b}{\sqrt{a^2 + b^2}} \).
Боковая поверхность второго конуса с образующей \( b \) равна \( S_{бок2} = \pi r b = \pi \frac{ab}{\sqrt{a^2 + b^2}} b = \frac{\pi ab^2}{\sqrt{a^2 + b^2}} \).
Площадь поверхности полученного тела равна сумме боковых поверхностей этих двух конусов:
\( S = S_{бок1} + S_{бок2} = \frac{\pi a^2b}{\sqrt{a^2 + b^2}} + \frac{\pi ab^2}{\sqrt{a^2 + b^2}} = \frac{\pi ab(a+b)}{\sqrt{a^2 + b^2}} \).

При вращении прямоугольного треугольника с катетами \( a \) и \( b \) вокруг его гипотенузы образуется тело, состоящее из двух конусов с общим основанием.

Основанием этих конусов является круг, полученный при вращении вершины прямого угла треугольника. Радиус \( r \) этого круга равен длине высоты, опущенной из вершины прямого угла на гипотенузу.

Длина гипотенузы прямоугольного треугольника с катетами \( a \) и \( b \) по теореме Пифагора равна \( \sqrt{a^2 + b^2} \).

Площадь прямоугольного треугольника может быть выражена как половина произведения катетов, то есть \( \frac{1}{2}ab \). Также площадь можно выразить как половина произведения гипотенузы на высоту, опущенную на нее, то есть \( \frac{1}{2}\sqrt{a^2 + b^2} \cdot r \).

Приравнивая эти выражения для площади, получаем \( \frac{1}{2}ab = \frac{1}{2}\sqrt{a^2 + b^2} \cdot r \). Из этого уравнения находим радиус общего основания конусов: \( r = \frac{ab}{\sqrt{a^2 + b^2}} \).

Образующими конусов являются катеты исходного прямоугольного треугольника. Для первого конуса образующая равна \( a \), а для второго конуса образующая равна \( b \).

Площадь боковой поверхности конуса вычисляется по формуле \( S_{бок} = \pi r L \), где \( r \) — радиус основания, а \( L \) — длина образующей.

Площадь боковой поверхности первого конуса с образующей \( a \) равна \( S_{бок1} = \pi \cdot \frac{ab}{\sqrt{a^2 + b^2}} \cdot a = \frac{\pi a^2b}{\sqrt{a^2 + b^2}} \).

Площадь боковой поверхности второго конуса с образующей \( b \) равна \( S_{бок2} = \pi \cdot \frac{ab}{\sqrt{a^2 + b^2}} \cdot b = \frac{\pi ab^2}{\sqrt{a^2 + b^2}} \).

Полная площадь поверхности полученного тела вращения равна сумме площадей боковых поверхностей этих двух конусов, так как основания конусов совпадают и находятся внутри тела.

Таким образом, площадь поверхности тела равна \( S = S_{бок1} + S_{бок2} = \frac{\pi a^2b}{\sqrt{a^2 + b^2}} + \frac{\pi ab^2}{\sqrt{a^2 + b^2}} \).

Вынося общий множитель \( \frac{\pi ab}{\sqrt{a^2 + b^2}} \), получаем \( S = \frac{\pi ab}{\sqrt{a^2 + b^2}} (a + b) = \frac{\pi ab(a+b)}{\sqrt{a^2 + b^2}} \).