
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 409 Атанасян — Подробные Ответы
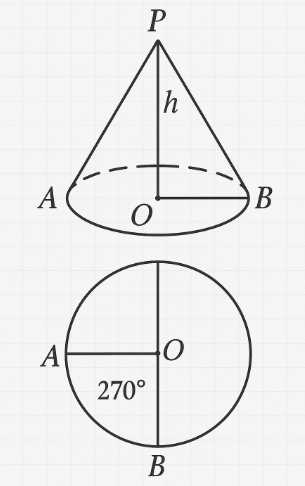
Найдите угол между образующей и высотой конуса, если развёрткой его боковой поверхности является сектор с дугой \(270^\circ\).
Решение:
По формуле развертки конуса имеем \(\frac{r}{L} = \frac{\alpha}{360^\circ}\), где \(r\) — радиус основания конуса, \(L\) — образующая, а \(\alpha\) — угол развертки.
Подставляя данное значение \(\alpha = 270^\circ\), получаем \(\frac{r}{L} = \frac{270^\circ}{360^\circ} = \frac{3}{4}\).
Рассмотрим прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей. Угол \(\beta\) между образующей и высотой конуса связан с отношением \(r\) к \(L\) соотношением \(\sin\beta = \frac{r}{L}\).
Следовательно, \(\sin\beta = \frac{3}{4}\).
Так как \(\beta\) является острым углом, то \(\beta = \arcsin\left(\frac{3}{4}\right)\).
Решение:
Для начала рассмотрим связь между параметрами конуса и его разверткой. Когда боковая поверхность конуса разворачивается на плоскость, она образует круговой сектор. Радиус этого сектора равен образующей конуса \(L\), а длина дуги сектора равна длине окружности основания конуса, которая составляет \(2\pi r\), где \(r\) — радиус основания конуса. Центральный угол \(\alpha\) этого сектора связан с длиной дуги и радиусом сектора формулой: длина дуги = \(\frac{\alpha}{360^\circ} \cdot 2\pi L\). Приравнивая длину дуги к длине окружности основания, получаем \(2\pi r = \frac{\alpha}{360^\circ} \cdot 2\pi L\). Сокращая \(2\pi\) с обеих сторон, приходим к соотношению \(\frac{r}{L} = \frac{\alpha}{360^\circ}\).
В условии задачи сказано, что разверткой боковой поверхности конуса является сектор с дугой \(270^\circ\). Это означает, что центральный угол сектора \(\alpha = 270^\circ\). Подставляя это значение в полученную формулу, находим отношение радиуса основания конуса к его образующей: \(\frac{r}{L} = \frac{270^\circ}{360^\circ}\). Упростим эту дробь, разделив числитель и знаменатель на их наибольший общий делитель, который равен \(90^\circ\). Получаем \(\frac{r}{L} = \frac{270 \div 90}{360 \div 90} = \frac{3}{4}\). Таким образом, отношение радиуса основания к образующей конуса равно \(\frac{3}{4}\).
Теперь рассмотрим прямоугольный треугольник, образованный высотой конуса \(h\), радиусом его основания \(r\) и образующей \(L\). Вершина конуса, центр основания и любая точка на окружности основания образуют такой треугольник, где прямой угол находится в центре основания. Угол между образующей и высотой конуса, который нам нужно найти, находится в этом прямоугольном треугольнике. Обозначим этот угол как \(\beta\). В этом прямоугольном треугольнике радиус основания \(r\) является катетом, противолежащим углу \(\beta\), а образующая \(L\) является гипотенузой. По определению синуса острого угла в прямоугольном треугольнике, синус угла равен отношению длины противолежащего катета к длине гипотенузы. Следовательно, \(\sin\beta = \frac{r}{L}\).
Из предыдущих вычислений мы знаем, что \(\frac{r}{L} = \frac{3}{4}\). Подставляя это значение в выражение для \(\sin\beta\), получаем \(\sin\beta = \frac{3}{4}\).
Чтобы найти значение угла \(\beta\), необходимо применить обратную тригонометрическую функцию к синусу, а именно арксинус. Арксинус числа — это угол, синус которого равен данному числу. Поскольку \(\beta\) является углом между высотой и образующей конуса, в контексте геометрии конуса этот угол всегда является острым (находится в пределах от \(0^\circ\) до \(90^\circ\)). Значение \(\frac{3}{4}\) находится между 0 и 1, что соответствует синусу острого угла. Следовательно, \(\beta = \arcsin\left(\frac{3}{4}\right)\). Это и есть искомый угол между образующей и высотой конуса.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!