ГДЗ по Геометрии 10 класс Номер 407 Атанасян — Подробные Ответы

Отношение площадей боковой и полной поверхностей конуса равно \(\frac{7}{8}\). Найдите угол между образующей и плоскостью основания конуса.

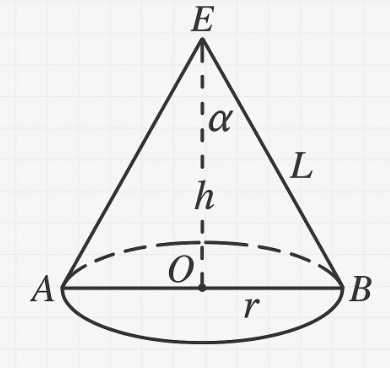
Пусть \(CO=h\), \(OB=r\), образующая \(L=\sqrt{h^2+r^2}\). Площадь боковой поверхности конуса \(S_{бок} = \pi r L = \pi r \sqrt{h^2+r^2}\). Площадь полной поверхности конуса \(S_{полн} = \pi r^2 + S_{бок} = \pi r^2 + \pi r \sqrt{h^2+r^2}\).

По условию отношение площадей боковой и полной поверхностей равно \(\frac{7}{8}\), то есть \(\frac{\pi r \sqrt{h^2+r^2}}{\pi r^2 + \pi r \sqrt{h^2+r^2}} = \frac{7}{8}\). Сокращая на \(\pi r\) (при условии \(r \neq 0\)), получаем \(\frac{\sqrt{h^2+r^2}}{r + \sqrt{h^2+r^2}} = \frac{7}{8}\). Умножая крест-накрест, имеем \(8\sqrt{h^2+r^2} = 7(r + \sqrt{h^2+r^2})\). Раскрывая скобки, получаем \(8\sqrt{h^2+r^2} = 7r + 7\sqrt{h^2+r^2}\). Вычитая \(7\sqrt{h^2+r^2}\) из обеих частей, находим \(\sqrt{h^2+r^2} = 7r\). Возводя обе части в квадрат, получаем \(h^2+r^2 = 49r^2\). Отсюда \(h^2 = 49r^2 — r^2 = 48r^2\). Разделим на \(r^2\) (при условии \(r \neq 0\)): \(\frac{h^2}{r^2} = 48\). Угол между образующей и плоскостью основания обозначим через \(\alpha\). В прямоугольном треугольнике, образованном высотой, радиусом основания и образующей, тангенс угла \(\alpha\) равен отношению противолежащего катета (высоты \(h\)) к прилежащему катету (радиусу \(r\)), то есть \(\tan \alpha = \frac{h}{r}\). Тогда \(\tan^2 \alpha = \frac{h^2}{r^2} = 48\). Используя тригонометрическое тождество \(1 + \tan^2 \alpha = \frac{1}{\cos^2 \alpha}\), подставляем значение \(\tan^2 \alpha\): \(1 + 48 = \frac{1}{\cos^2 \alpha}\), что дает \(49 = \frac{1}{\cos^2 \alpha}\). Следовательно, \(\cos^2 \alpha = \frac{1}{49}\). Извлекая квадратный корень, получаем \(\cos \alpha = \pm \frac{1}{7}\). Поскольку угол \(\alpha\) является острым углом в прямоугольном треугольнике, его косинус должен быть положительным. Таким образом, \(\cos \alpha = \frac{1}{7}\). Угол \(\alpha\) равен арккосинусу \(\frac{1}{7}\), то есть \(\alpha = \arccos \frac{1}{7}\).

Пусть высота конуса равна \(h\), радиус основания равен \(r\), а образующая равна \(L\). Из прямоугольного треугольника, образованного высотой, радиусом и образующей, по теореме Пифагора имеем \(L = \sqrt{h^2+r^2}\). Площадь боковой поверхности конуса вычисляется по формуле \(S_{бок} = \pi r L = \pi r \sqrt{h^2+r^2}\). Площадь основания конуса равна \(S_{осн} = \pi r^2\).

Площадь полной поверхности конуса равна сумме площади основания и площади боковой поверхности: \(S_{полн} = S_{осн} + S_{бок} = \pi r^2 + \pi r \sqrt{h^2+r^2}\). По условию задачи отношение площади боковой поверхности к площади полной поверхности равно \(\frac{7}{8}\). Запишем это в виде уравнения: \(\frac{S_{бок}}{S_{полн}} = \frac{\pi r \sqrt{h^2+r^2}}{\pi r^2 + \pi r \sqrt{h^2+r^2}} = \frac{7}{8}\). Заметим, что в числителе и знаменателе присутствует общий множитель \(\pi r\) (предполагая, что радиус \(r > 0\)). Сократим на \(\pi r\): \(\frac{\sqrt{h^2+r^2}}{r + \sqrt{h^2+r^2}} = \frac{7}{8}\). Теперь умножим обе части уравнения крест-накрест: \(8 \cdot \sqrt{h^2+r^2} = 7 \cdot (r + \sqrt{h^2+r^2})\). Раскроем скобки в правой части уравнения: \(8 \sqrt{h^2+r^2} = 7r + 7 \sqrt{h^2+r^2}\). Перенесем слагаемое \(7 \sqrt{h^2+r^2}\) из правой части в левую, изменив знак: \(8 \sqrt{h^2+r^2} — 7 \sqrt{h^2+r^2} = 7r\). Упростим левую часть: \(\sqrt{h^2+r^2} = 7r\). Возведем обе части последнего уравнения в квадрат, чтобы избавиться от квадратного корня: \((\sqrt{h^2+r^2})^2 = (7r)^2\), что дает \(h^2+r^2 = 49r^2\). Вычтем \(r^2\) из обеих частей уравнения: \(h^2 = 49r^2 — r^2\), откуда получаем \(h^2 = 48r^2\). Разделим обе части на \(r^2\) (поскольку \(r > 0\), \(r^2 > 0\)): \(\frac{h^2}{r^2} = \frac{48r^2}{r^2}\), что упрощается до \(\frac{h^2}{r^2} = 48\). Угол между образующей и плоскостью основания конуса обозначим через \(\alpha\). В прямоугольном треугольнике, образованном высотой конуса, радиусом основания и образующей, тангенс угла \(\alpha\) равен отношению противолежащего катета (высоты \(h\)) к прилежащему катету (радиусу \(r\)): \(\tan \alpha = \frac{h}{r}\). Тогда \(\tan^2 \alpha = \left(\frac{h}{r}\right)^2 = \frac{h^2}{r^2}\). Подставим найденное значение \(\frac{h^2}{r^2} = 48\): \(\tan^2 \alpha = 48\). Воспользуемся основным тригонометрическим тождеством, связывающим тангенс и косинус: \(1 + \tan^2 \alpha = \frac{1}{\cos^2 \alpha}\). Подставим значение \(\tan^2 \alpha = 48\): \(1 + 48 = \frac{1}{\cos^2 \alpha}\), что дает \(49 = \frac{1}{\cos^2 \alpha}\). Отсюда выразим \(\cos^2 \alpha\): \(\cos^2 \alpha = \frac{1}{49}\). Извлечем квадратный корень из обеих частей: \(\cos \alpha = \pm \sqrt{\frac{1}{49}} = \pm \frac{1}{7}\). Угол \(\alpha\) является углом между образующей и плоскостью основания конуса. В контексте геометрии конуса, этот угол всегда острый (если только конус не вырожденный, что не предполагается условием задачи). Для острого угла косинус всегда положителен. Следовательно, мы выбираем положительное значение: \(\cos \alpha = \frac{1}{7}\). Сам угол \(\alpha\) находится как арккосинус этого значения: \(\alpha = \arccos \frac{1}{7}\).