Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 406 Атанасян — Подробные Ответы
Площадь основания конуса равна S\(_1\), а площадь боковой поверхности равна S\(_0\). Найдите площадь осевого сечения конуса.
Дано: Площадь основания \(S_{осн} = S_1\), площадь боковой поверхности \(S_{бок} = S_0\).
Найти: Площадь осевого сечения.
Решение:
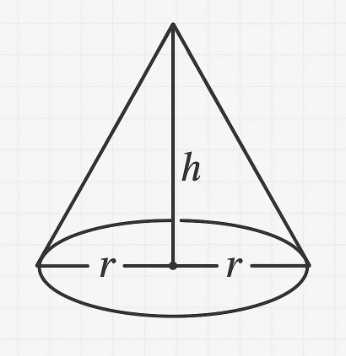
Пусть \(r\) — радиус основания конуса, \(h\) — высота конуса, \(L\) — образующая конуса.
Площадь основания конуса \(S_1 = \pi r^2\).
Площадь боковой поверхности конуса \(S_0 = \pi r L\).
Образующая связана с радиусом и высотой соотношением \(L = \sqrt{h^2 + r^2}\).
Площадь осевого сечения конуса равна \(rh\).
Из \(S_1 = \pi r^2\) следует \(r^2 = \frac{S_1}{\pi}\).
Из \(S_0 = \pi r L\) и \(L = \sqrt{h^2 + r^2}\) получаем \(S_0 = \pi r \sqrt{h^2 + r^2}\).
Возведем обе части в квадрат: \(S_0^2 = \pi^2 r^2 (h^2 + r^2)\).
Раскроем скобки: \(S_0^2 = \pi^2 r^2 h^2 + \pi^2 r^4\).
Так как \(S_1 = \pi r^2\), то \(S_1^2 = \pi^2 r^4\).
Подставим \(S_1^2\) в выражение для \(S_0^2\): \(S_0^2 = \pi^2 r^2 h^2 + S_1^2\).
Выразим \(r^2 h^2\): \(r^2 h^2 = S_0^2 — S_1^2\).
Разделим на \(\pi^2\): \(r^2 h^2 = \frac{S_0^2 — S_1^2}{\pi^2}\).
Извлечем квадратный корень: \(rh = \sqrt{\frac{S_0^2 — S_1^2}{\pi^2}} = \frac{\sqrt{S_0^2 — S_1^2}}{\pi}\).
Площадь осевого сечения равна \(\frac{\sqrt{S_0^2 — S_1^2}}{\pi}\).
Дано: Площадь основания конуса \(S_{осн} = S_1\), площадь боковой поверхности конуса \(S_{бок} = S_0\).
Найти: Площадь осевого сечения конуса.
Решение:
Введем обозначения: пусть \(r\) — радиус основания конуса, \(h\) — высота конуса, а \(L\) — образующая конуса.
По условию, площадь основания конуса \(S_1\) выражается формулой \(S_1 = \pi r^2\).
Также по условию, площадь боковой поверхности конуса \(S_0\) выражается формулой \(S_0 = \pi r L\).
Образующая конуса \(L\) связана с радиусом основания \(r\) и высотой конуса \(h\) соотношением, следующим из теоремы Пифагора для прямоугольного треугольника, образованного радиусом, высотой и образующей: \(L = \sqrt{h^2 + r^2}\).
Площадь осевого сечения конуса представляет собой площадь равнобедренного треугольника с основанием \(2r\) (диаметр основания конуса) и высотой \(h\). Формула для площади этого треугольника: \(\frac{1}{2} \times \text{основание} \times \text{высота} = \frac{1}{2} \times (2r) \times h = rh\). Наша задача — найти значение произведения \(rh\).
Используем данные нам площади \(S_1\) и \(S_0\).
Из формулы для площади боковой поверхности \(S_0 = \pi r L\) подставим выражение для \(L\):
\(S_0 = \pi r \sqrt{h^2 + r^2}\).
Чтобы избавиться от квадратного корня, возведем обе части этого уравнения в квадрат:
\(S_0^2 = (\pi r \sqrt{h^2 + r^2})^2\).
\(S_0^2 = \pi^2 r^2 (h^2 + r^2)\).
Теперь раскроем скобки в правой части уравнения:
\(S_0^2 = \pi^2 r^2 h^2 + \pi^2 r^2 r^2\).
\(S_0^2 = \pi^2 r^2 h^2 + \pi^2 r^4\).
Рассмотрим формулу для площади основания \(S_1 = \pi r^2\). Если возвести это уравнение в квадрат, получим:
\(S_1^2 = (\pi r^2)^2\).
\(S_1^2 = \pi^2 (r^2)^2\).
\(S_1^2 = \pi^2 r^4\).
Теперь мы можем подставить выражение для \(\pi^2 r^4\) из формулы для \(S_1^2\) в уравнение для \(S_0^2\):
\(S_0^2 = \pi^2 r^2 h^2 + S_1^2\).
Наша цель — найти \(rh\). В полученном уравнении у нас есть член \(\pi^2 r^2 h^2\), который можно записать как \(\pi^2 (rh)^2\).
Выразим \(\pi^2 r^2 h^2\) из уравнения:
\(\pi^2 r^2 h^2 = S_0^2 — S_1^2\).
Теперь выразим \(r^2 h^2\), разделив обе части уравнения на \(\pi^2\):
\(r^2 h^2 = \frac{S_0^2 — S_1^2}{\pi^2}\).
Левая часть \(r^2 h^2\) — это квадрат произведения \(rh\), то есть \((rh)^2\).
\((rh)^2 = \frac{S_0^2 — S_1^2}{\pi^2}\).
Чтобы найти \(rh\), извлечем квадратный корень из обеих частей уравнения. Поскольку \(r\) и \(h\) — положительные величины (радиус и высота конуса), их произведение \(rh\) также положительно.
\(rh = \sqrt{\frac{S_0^2 — S_1^2}{\pi^2}}\).
Извлекая корень из знаменателя, получаем:
\(rh = \frac{\sqrt{S_0^2 — S_1^2}}{\sqrt{\pi^2}}\).
\(rh = \frac{\sqrt{S_0^2 — S_1^2}}{\pi}\).
Произведение \(rh\) равно площади осевого сечения конуса.
Таким образом, площадь осевого сечения конуса выражается формулой \(\frac{\sqrt{S_0^2 — S_1^2}}{\pi}\).
Это и есть площадь осевого сечения.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.