ГДЗ по Геометрии 10 класс Номер 405 Атанасян — Подробные Ответы

Найдите косинус угла при вершине осевого сечения конуса, имеющего три попарно перпендикулярные образующие.

Пусть образующие конуса \(DA, DB, DC\) попарно перпендикулярны и имеют длину \(a\). Тогда треугольники \(DAB, DBC, DAC\) являются прямоугольными с катетами \(a\). Стороны основания \(AB, BC, AC\) являются гипотенузами этих треугольников.

\(AB = BC = AC = \sqrt{a^2 + a^2} = a\sqrt{2}\).
Основание конуса — окружность, описанная вокруг равностороннего треугольника \(ABC\). Радиус \(R\) этой окружности равен \(\frac{AB}{\sqrt{3}} = \frac{a\sqrt{2}}{\sqrt{3}} = a\sqrt{\frac{2}{3}}\).
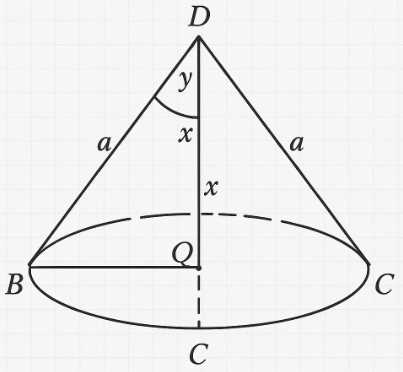
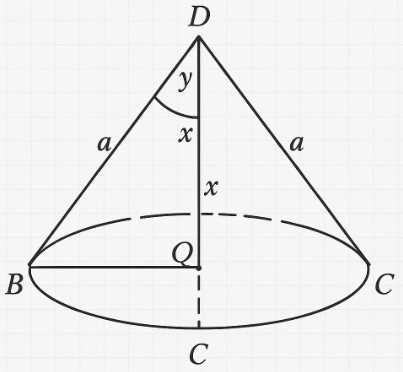
Осевое сечение конуса представляет собой равнобедренный треугольник, образованный вершиной \(D\) и диаметром основания. Длина диаметра равна \(2R = 2a\sqrt{\frac{2}{3}}\).
Рассмотрим осевое сечение — треугольник, образованный вершиной \(D\) и диаметром основания длиной \(2a\sqrt{\frac{2}{3}}\). Боковые стороны этого треугольника — образующие конуса, их длина равна \(a\).
Пусть \(\alpha\) — угол при вершине осевого сечения. По теореме косинусов для этого треугольника имеем:
\((2a\sqrt{\frac{2}{3}})^2 = a^2 + a^2 — 2 \cdot a \cdot a \cos \alpha\)
\(4a^2 \cdot \frac{2}{3} = 2a^2 — 2a^2 \cos \alpha\)
\(\frac{8}{3}a^2 = 2a^2 (1 — \cos \alpha)\)
\(\frac{4}{3} = 1 — \cos \alpha\)
\(\cos \alpha = 1 — \frac{4}{3} = -\frac{1}{3}\).
Косинус угла при вершине осевого сечения равен \(-\frac{1}{3}\).

Решение:
Пусть даны три попарно перпендикулярные образующие конуса \(DA, DB, DC\). Пусть их длина равна \(a\).
Так как образующие \(DA, DB\) перпендикулярны, треугольник \(DAB\) является прямоугольным с прямым углом при вершине \(D\). Аналогично, треугольники \(DBC\) и \(DAC\) являются прямоугольными с прямым углом при вершине \(D\).

Стороны основания конуса являются гипотенузами этих прямоугольных треугольников. Найдем длины сторон треугольника \(ABC\) по теореме Пифагора:
\(AB = \sqrt{DA^2 + DB^2} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2}\).
\(BC = \sqrt{DB^2 + DC^2} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2}\).
\(AC = \sqrt{DA^2 + DC^2} = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2}\).
Таким образом, треугольник \(ABC\) является равносторонним со стороной \(a\sqrt{2}\).
Основание конуса представляет собой окружность, описанную вокруг равностороннего треугольника \(ABC\). Найдем радиус \(R\) этой описанной окружности. По теореме синусов для треугольника \(ABC\), отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности:
\(\frac{AB}{\sin \angle ACB} = 2R\).
Так как треугольник \(ABC\) равносторонний, все его углы равны \(60^\circ\).
\(\frac{a\sqrt{2}}{\sin 60^\circ} = 2R\).
\(\frac{a\sqrt{2}}{\frac{\sqrt{3}}{2}} = 2R\).
\(\frac{2a\sqrt{2}}{\sqrt{3}} = 2R\).
\(R = \frac{a\sqrt{2}}{\sqrt{3}} = a\sqrt{\frac{2}{3}}\).
Осевое сечение конуса представляет собой равнобедренный треугольник, вершиной которого является вершина конуса \(D\), а основанием — диаметр окружности основания. Длина боковых сторон этого треугольника равна длине образующей конуса, то есть \(a\). Длина основания равна диаметру окружности основания, который равен \(2R\).
Пусть \(BF\) — диаметр основания, тогда \(BF = 2R = 2a\sqrt{\frac{2}{3}}\).
Рассмотрим осевое сечение — треугольник \(BDF\), где \(D\) — вершина конуса, а \(BF\) — диаметр основания. Стороны этого треугольника имеют длины \(DB = a\), \(DF = a\) (так как \(DF\) также является образующей) и \(BF = 2a\sqrt{\frac{2}{3}}\).
Пусть \(\alpha\) — угол при вершине осевого сечения, то есть \(\angle BDF = \alpha\). Применим теорему косинусов к треугольнику \(BDF\):
\(BF^2 = DB^2 + DF^2 — 2 \cdot DB \cdot DF \cos \alpha\).
\((2a\sqrt{\frac{2}{3}})^2 = a^2 + a^2 — 2 \cdot a \cdot a \cos \alpha\).
\(4a^2 \cdot \frac{2}{3} = 2a^2 — 2a^2 \cos \alpha\).
\(\frac{8}{3}a^2 = 2a^2 (1 — \cos \alpha)\).
Разделим обе части уравнения на \(2a^2\) (при условии \(a \neq 0\)):
\(\frac{4}{3} = 1 — \cos \alpha\).
Выразим \(\cos \alpha\):
\(\cos \alpha = 1 — \frac{4}{3}\).
\(\cos \alpha = -\frac{1}{3}\).
Таким образом, косинус угла при вершине осевого сечения конуса равен \(-\frac{1}{3}\).