
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 403 Атанасян — Подробные Ответы
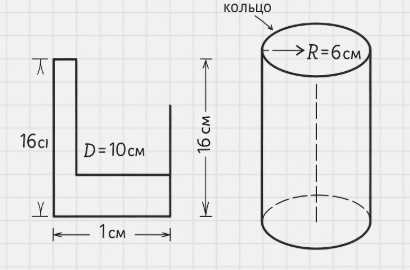
Толщина боковой стенки и дна стакана цилиндрической формы равна 1 см, высота стакана равна 16 см, а внутренний радиус равен 5 см. Вычислите площадь полной поверхности стакана.
Внутренний радиус стакана равен 5 см, значит внутренний диаметр \(D = 10\) см. Внешний диаметр с учетом толщины стенок 1 см будет \(10 + 2 \times 1 = 12\) см, а внешний радиус 6 см. Площадь внешнего дна равна \(S_{осн.внеш} = \pi \times 6^2 = 36\pi\) см². Высота стакана 16 см. Площадь внешней боковой поверхности равна \(S_{бок.внеш} = 2\pi \times 6 \times 16 = 192\pi\) см². Площадь внешней поверхности стакана равна \(S_{внеш} = S_{бок.внеш} + S_{осн.внеш} = 192\pi + 36\pi = 228\pi\) см².
Площадь внутреннего дна равна \(S_{осн.внутр} = \pi \times 5^2 = 25\pi\) см². Высота внутренней части стакана с учетом толщины дна 1 см равна \(16 — 1 = 15\) см. Площадь внутренней боковой поверхности равна \(S_{бок.внутр} = 2\pi \times 5 \times 15 = 150\pi\) см². Площадь внутренней поверхности стакана равна \(S_{внутр} = S_{осн.внутр} + S_{бок.внутр} = 25\pi + 150\pi = 175\pi\) см².
Площадь верхнего кольца (торца стенки) равна разности площадей внешнего и внутреннего кругов: \(S_{кольца} = \pi \times (6^2 — 5^2) = \pi \times (36 — 25) = 11\pi\) см².
Площадь полной поверхности стакана равна сумме площадей внешней поверхности, внутренней поверхности и верхнего кольца: \(S_{полная} = S_{внеш} + S_{внутр} + S_{кольца} = 228\pi + 175\pi + 11\pi = 414\pi\) см².
Внутренний радиус стакана равен 5 см.
Внутренний диаметр \(D\) равен удвоенному внутреннему радиусу: \(D = 2 \times 5 = 10\) см.
Толщина стенок и дна стакана равна 1 см.
Внешний диаметр стакана равен внутреннему диаметру плюс удвоенная толщина стенки: \(D_{внеш} = 10 + 2 \times 1 = 12\) см.
Внешний радиус стакана равен половине внешнего диаметра: \(R_{внеш} = 12 / 2 = 6\) см.
Найдем площадь внешней поверхности стакана.
Площадь внешнего дна стакана (круг с внешним радиусом) рассчитывается по формуле площади круга \(S = \pi r^2\): \(S_{осн.внеш} = \pi \times R_{внеш}^2 = \pi \times 6^2 = 36\pi\) см².
Высота стакана равна 16 см.
Площадь внешней боковой поверхности стакана (цилиндр с внешним радиусом и высотой) рассчитывается по формуле \(S = 2\pi r h\): \(S_{бок.внеш} = 2\pi \times R_{внеш} \times h = 2\pi \times 6 \times 16 = 192\pi\) см².
Площадь всей внешней поверхности стакана равна сумме площади внешнего дна и площади внешней боковой поверхности: \(S_{внеш} = S_{осн.внеш} + S_{бок.внеш} = 36\pi + 192\pi = 228\pi\) см².
Теперь найдем площадь внутренней поверхности стакана.
Внутренний радиус стакана равен 5 см.
Площадь внутреннего дна стакана (круг с внутренним радиусом) рассчитывается по формуле площади круга \(S = \pi r^2\): \(S_{осн.внутр} = \pi \times 5^2 = 25\pi\) см².
Высота внутренней части стакана меньше общей высоты на толщину дна: \(h_{внутр} = 16 — 1 = 15\) см.
Площадь внутренней боковой поверхности стакана (цилиндр с внутренним радиусом и внутренней высотой) рассчитывается по формуле \(S = 2\pi r h\): \(S_{бок.внутр} = 2\pi \times 5 \times 15 = 150\pi\) см².
Площадь всей внутренней поверхности стакана равна сумме площади внутреннего дна и площади внутренней боковой поверхности: \(S_{внутр} = S_{осн.внутр} + S_{бок.внутр} = 25\pi + 150\pi = 175\pi\) см².
Далее найдем площадь верхнего кольца (торца стенки стакана). Это разность площадей кругов с внешним и внутренним радиусами: \(S_{кольца} = \pi R_{внеш}^2 — \pi r_{внутр}^2 = \pi \times (R_{внеш}^2 — r_{внутр}^2) = \pi \times (6^2 — 5^2) = \pi \times (36 — 25) = 11\pi\) см².
Наконец, вычислим площадь полной поверхности стакана. Она состоит из площади внешней поверхности, площади внутренней поверхности и площади верхнего кольца: \(S_{полная} = S_{внеш} + S_{внутр} + S_{кольца} = 228\pi + 175\pi + 11\pi = 403\pi + 11\pi = 414\pi\) см².
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!