Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 399 Атанасян — Подробные Ответы
При вращении прямоугольника вокруг неравных сторон получаются цилиндры, площади полных поверхностей которых равны S\(_1\) и S\(_2\). Найдите диагональ прямоугольника.
При вращении прямоугольника со сторонами \(a\) и \(b\) вокруг стороны \(a\) получаем цилиндр с радиусом \(b\) и высотой \(a\). Площадь его полной поверхности равна \(S_1 = 2\pi ab + 2\pi b^2\).
При вращении прямоугольника вокруг стороны \(b\) получаем цилиндр с радиусом \(a\) и высотой \(b\). Площадь его полной поверхности равна \(S_2 = 2\pi ab + 2\pi a^2\).
Из системы уравнений \(2\pi b(a+b) = S_1\) и \(2\pi a(a+b) = S_2\) следует \(\frac{b}{a} = \frac{S_1}{S_2}\).
Подставляя \(b = a \frac{S_1}{S_2}\) в первое уравнение, получаем \(2\pi a (a \frac{S_1}{S_2}) + 2\pi (a \frac{S_1}{S_2})^2 = S_1\), что приводит к \(a^2 = \frac{S_2^2}{2\pi (S_1 + S_2)}\).
Тогда \(b^2 = a^2 (\frac{S_1}{S_2})^2 = \frac{S_2^2}{2\pi (S_1 + S_2)} \frac{S_1^2}{S_2^2} = \frac{S_1^2}{2\pi (S_1 + S_2)}\).
Диагональ прямоугольника \(BD\) находится по теореме Пифагора: \(BD = \sqrt{a^2 + b^2} = \sqrt{\frac{S_2^2}{2\pi (S_1 + S_2)} + \frac{S_1^2}{2\pi (S_1 + S_2)}} = \sqrt{\frac{S_1^2 + S_2^2}{2\pi (S_1 + S_2)}}\).
Пусть стороны прямоугольника равны \(a\) и \(b\).
При вращении прямоугольника вокруг стороны длиной \(a\) (например, стороны AB), получается цилиндр с радиусом основания \(r = b\) и высотой \(L = a\). Площадь полной поверхности этого цилиндра \(S_1\) вычисляется по формуле \(S = 2\pi r L + 2\pi r^2\). Подставляя значения \(r\) и \(L\), получаем \(S_1 = 2\pi b a + 2\pi b^2 = 2\pi b(a+b)\).
При вращении прямоугольника вокруг стороны длиной \(b\) (например, стороны AD), получается цилиндр с радиусом основания \(r = a\) и высотой \(L = b\). Площадь полной поверхности этого цилиндра \(S_2\) вычисляется по той же формуле \(S = 2\pi r L + 2\pi r^2\). Подставляя значения \(r\) и \(L\), получаем \(S_2 = 2\pi a b + 2\pi a^2 = 2\pi a(b+a)\).
По условию задачи площади полных поверхностей равны \(S_1\) и \(S_2\), что дает нам систему уравнений:
\(S_1 = 2\pi b(a+b)\)
\(S_2 = 2\pi a(a+b)\)
Разделим первое уравнение на второе, предполагая, что \(a, b > 0\) и \(a+b > 0\):
\(\frac{S_1}{S_2} = \frac{2\pi b(a+b)}{2\pi a(a+b)}\)
\(\frac{S_1}{S_2} = \frac{b}{a}\)
Из этого соотношения выразим \(b\) через \(a\), \(S_1\) и \(S_2\): \(b = a \frac{S_1}{S_2}\).
Подставим полученное выражение для \(b\) в первое уравнение системы:
\(S_1 = 2\pi (a \frac{S_1}{S_2})(a + a \frac{S_1}{S_2})\)
Вынесем \(a\) из скобки:
\(S_1 = 2\pi a \frac{S_1}{S_2} a (1 + \frac{S_1}{S_2})\)
\(S_1 = 2\pi a^2 \frac{S_1}{S_2} (\frac{S_2 + S_1}{S_2})\)
\(S_1 = 2\pi a^2 \frac{S_1 (S_1 + S_2)}{S_2^2}\)
Теперь выразим \(a^2\) из этого уравнения:
\(a^2 = \frac{S_1 S_2^2}{2\pi S_1 (S_1 + S_2)}\)
Сократим \(S_1\) в числителе и знаменателе (при условии \(S_1 \neq 0\)):
\(a^2 = \frac{S_2^2}{2\pi (S_1 + S_2)}\)
Теперь найдем \(b^2\), используя соотношение \(b = a \frac{S_1}{S_2}\):
\(b^2 = (a \frac{S_1}{S_2})^2 = a^2 \frac{S_1^2}{S_2^2}\)
Подставим ранее найденное выражение для \(a^2\):
\(b^2 = \frac{S_2^2}{2\pi (S_1 + S_2)} \frac{S_1^2}{S_2^2}\)
Сократим \(S_2^2\) в числителе и знаменателе (при условии \(S_2 \neq 0\)):
\(b^2 = \frac{S_1^2}{2\pi (S_1 + S_2)}\)
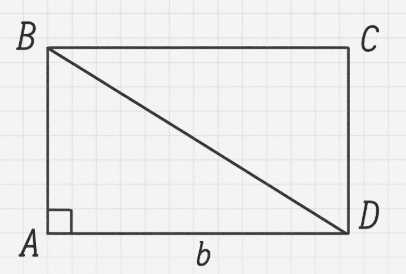
Диагональ прямоугольника \(BD\) является гипотенузой прямоугольного треугольника ABD со катетами \(a\) и \(b\). По теореме Пифагора, квадрат диагонали равен сумме квадратов сторон: \(BD^2 = a^2 + b^2\).
Следовательно, \(BD = \sqrt{a^2 + b^2}\).
Подставим найденные выражения для \(a^2\) и \(b^2\) в формулу для диагонали:
\(BD = \sqrt{\frac{S_2^2}{2\pi (S_1 + S_2)} + \frac{S_1^2}{2\pi (S_1 + S_2)}}\)
Сложим дроби под корнем, так как у них одинаковый знаменатель:
\(BD = \sqrt{\frac{S_2^2 + S_1^2}{2\pi (S_1 + S_2)}}\)
Таким образом, диагональ прямоугольника равна \(\sqrt{\frac{S_1^2 + S_2^2}{2\pi (S_1 + S_2)}}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.