
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 398 Атанасян — Подробные Ответы
Докажите, что если плоскость параллельна оси цилиндра и расстояние между этой плоскостью и осью равно радиусу цилиндра, то плоскость содержит образующую цилиндра, и притом только одну. (В этом случае плоскость называется касательной плоскостью к цилиндру.)
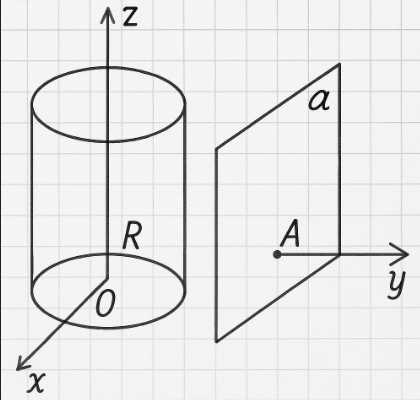
Возьмем систему координат так, что ось ординат перпендикулярна плоскости \( \alpha \), а ось аппликат направлена по оси цилиндра. Будем приближать плоскость \( \alpha \) к оси \( Ox \) параллельно плоскости \( Oxz \). Когда расстояние станет равно \( R \), то допустим, что через точку \( A \) можно провести две прямые, параллельные оси \( Ox \) (или, что то же самое, перпендикулярные плоскости \( Oxy \)). Но по теореме п.4 через точку \( A \) может проходить только одна прямая, параллельная оси цилиндра. Значит, на поверхности цилиндра найдется только одна прямая, лежащая в плоскости \( \alpha \) и параллельная оси цилиндра, она и есть образующая цилиндра.
Доказательство начинается с выбора удобной системы координат. Возьмем систему координат таким образом, чтобы ось ординат была перпендикулярна плоскости \( \alpha \). Ось аппликат \( Oz \) направим вдоль оси цилиндра. Таким образом, ось цилиндра совпадает с осью \( Oz \).
Теперь рассмотрим плоскость \( \alpha \). По условию, она параллельна оси цилиндра, то есть оси \( Oz \). Также по условию, расстояние от этой плоскости до оси цилиндра (оси \( Oz \)) равно радиусу цилиндра \( R \).
Представим, что мы приближаем плоскость \( \alpha \) к оси \( Ox \) параллельно плоскости \( Oxz \). Плоскость \( Oxz \) содержит ось \( Ox \) и ось \( Oz \). Поскольку плоскость \( \alpha \) параллельна оси \( Oz \), она может быть параллельна плоскости \( Oxz \) в определенном смысле, или, точнее, мы можем рассматривать ее положение относительно оси \( Ox \) в плоскости \( Oxy \).
Когда расстояние от плоскости \( \alpha \) до оси \( Oz \) становится равным радиусу цилиндра \( R \), плоскость \( \alpha \) касается цилиндра. Рассмотрим точку \( A \) на поверхности цилиндра, которая также лежит в плоскости \( \alpha \).
Допустим, что через эту точку \( A \) можно провести две различные прямые, которые лежат на поверхности цилиндра и параллельны оси цилиндра (оси \( Oz \)). Прямые, параллельные оси \( Oz \), также параллельны оси \( Ox \) в проекции на плоскость \( Oxy \), или, что то же самое, перпендикулярны плоскости \( Oxy \).
Однако, согласно теореме п.4 (которая, предположительно, утверждает уникальность прямой, проходящей через данную точку и параллельной данной прямой или оси в контексте цилиндрических поверхностей), через точку \( A \) на поверхности цилиндра, параллельно оси цилиндра, может проходить только одна прямая.
Это противоречит нашему допущению о существовании двух таких прямых. Следовательно, наше допущение неверно.
Таким образом, на поверхности цилиндра найдется только одна прямая, которая одновременно лежит в плоскости \( \alpha \) и параллельна оси цилиндра. Эта единственная прямая по определению является образующей цилиндра. Поскольку плоскость \( \alpha \) содержит эту образующую и касается цилиндра (расстояние до оси равно \( R \)), плоскость \( \alpha \) является касательной плоскостью к цилиндру.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!