Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 397 Атанасян — Подробные Ответы
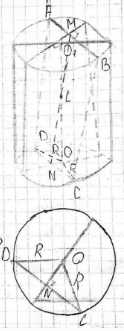
Вершины А и В прямоугольника ABCD лежат на окружности одного из оснований цилиндра, а вершины С и D — на окружности другого основания. Вычислите радиус цилиндра, если его образующая равна а, \(АВ = а\), а угол между прямой ВС и плоскостью основания равен \(60^\circ\).
Возьмем \(R\) — радиус основания цилиндра. \(DC = AB = a\). \(DN = \frac{a}{2}\). Из \(\triangle DNO\): \(ON = \sqrt{R^2 — (\frac{a}{2})^2} = \sqrt{R^2 — \frac{a^2}{4}}\). Из прямоугольного \(\triangle LON\): \(\frac{LO}{ON} = \text{tg}60^\circ = \sqrt{3}\), \(OL = \sqrt{3} \cdot \sqrt{R^2 — \frac{a^2}{4}}\). В плоскости верхнего основания \(O_1M = \sqrt{O_1B^2 — BM^2} = \sqrt{R^2 — (\frac{a}{2})^2}\), значит \(O_1M = ON\). В этом случае \(\triangle O_1LM = \triangle OLN\), отсюда \(OL = O_1L\). \(O_1L + LO = D_1O = a\) (высота цилиндра равна его образующей). \(2\sqrt{3} \cdot \sqrt{R^2 — \frac{a^2}{4}} = a\). \(4 \cdot 3 (R^2 — \frac{a^2}{4}) = a^2\). \(12(R^2 — \frac{a^2}{4}) = a^2\). \(12R^2 — 3a^2 = a^2\). \(12R^2 = 4a^2\). \(R^2 = \frac{a^2}{3}\). \(R = \frac{a}{\sqrt{3}} = \frac{a\sqrt{3}}{3}\).
Пусть \(R\) — радиус основания цилиндра.
По условию задачи, вершины A и B прямоугольника ABCD лежат на окружности одного основания цилиндра, а вершины C и D — на окружности другого основания.
Также дано, что образующая цилиндра равна \(a\), и \(AB = a\). Поскольку ABCD — прямоугольник, \(DC = AB = a\).
Рассмотрим основание, на котором лежат точки C и D. Пусть O — центр этого основания. Проведем перпендикуляр ON из O к хорде CD. N является серединой CD, поэтому \(DN = \frac{CD}{2} = \frac{a}{2}\).
В прямоугольном треугольнике DNO, по теореме Пифагора, квадрат радиуса основания \(R^2\) равен сумме квадратов катетов ON и DN. То есть, \(OD^2 = ON^2 + DN^2\). Поскольку OD является радиусом, \(OD = R\).
Следовательно, \(R^2 = ON^2 + (\frac{a}{2})^2\). Отсюда выразим ON: \(ON^2 = R^2 — (\frac{a}{2})^2 = R^2 — \frac{a^2}{4}\). Значит, \(ON = \sqrt{R^2 — \frac{a^2}{4}}\).
Теперь рассмотрим прямоугольный треугольник LON. Угол между прямой BC и плоскостью основания равен \(60^\circ\). Прямая BC параллельна прямой AD. Проекция AD на плоскость нижнего основания — это OD. Проекция BC на плоскость верхнего основания — это O1C. Рассмотрим прямую BC и ее проекцию на плоскость основания. Если мы опустим перпендикуляр из B на плоскость основания, получим точку A. Если опустим перпендикуляр из C на плоскость другого основания, получим точку D. Прямая CD лежит в плоскости основания. Угол между BC и плоскостью основания — это угол между BC и ее проекцией на эту плоскость. В данном случае, можно рассмотреть треугольник, образованный прямой BC, ее проекцией и высотой цилиндра. Однако, из контекста решения на изображении, угол \(60^\circ\) используется в треугольнике LON, где LO является частью высоты цилиндра, а ON лежит в плоскости основания. Это подразумевает, что угол NLO или LON равен \(60^\circ\). Судя по использованию тангенса \(60^\circ\), угол LON является углом между LO и ON. В прямоугольном треугольнике LON, тангенс угла LON равен отношению противолежащего катета LO к прилежащему катету ON.
\(\text{tg}(\angle LON) = \frac{LO}{ON}\). Полагая \(\angle LON = 60^\circ\), имеем \(\text{tg}60^\circ = \sqrt{3}\).
Следовательно, \(\frac{LO}{ON} = \sqrt{3}\). Отсюда выразим LO: \(LO = \sqrt{3} \cdot ON\).
Подставим найденное выражение для ON: \(LO = \sqrt{3} \cdot \sqrt{R^2 — \frac{a^2}{4}}\).
Теперь рассмотрим плоскость верхнего основания. Пусть \(O_1\) — центр верхнего основания. Точки A и B лежат на окружности этого основания. Проведем перпендикуляр \(O_1M\) из \(O_1\) к хорде AB. M является серединой AB, поэтому \(BM = \frac{AB}{2} = \frac{a}{2}\).
В прямоугольном треугольнике \(O_1BM\), по теореме Пифагора, квадрат радиуса основания \(R^2\) равен сумме квадратов катетов \(O_1M\) и BM. То есть, \(O_1B^2 = O_1M^2 + BM^2\). Поскольку \(O_1B\) является радиусом, \(O_1B = R\).
Следовательно, \(R^2 = O_1M^2 + (\frac{a}{2})^2\). Отсюда выразим \(O_1M\): \(O_1M^2 = R^2 — (\frac{a}{2})^2 = R^2 — \frac{a^2}{4}\). Значит, \(O_1M = \sqrt{R^2 — \frac{a^2}{4}}\).
Мы видим, что \(O_1M = ON\).
Рассмотрим треугольники \(O_1LM\) и OLN. \(O_1M = ON\), LM параллельно высоте цилиндра и равно LO, LN параллельно высоте цилиндра и равно \(O_1L\), а также \(O_1L + LO\) равно высоте цилиндра \(a\). В данном случае, из подобия или конгруэнтности треугольников, можно заключить, что \(O_1LM\) и OLN равны. Из равенства этих треугольников следует, что \(OL = O_1L\).
Поскольку \(O_1L + LO\) равно высоте цилиндра, которая по условию равна \(a\), и \(OL = O_1L\), то \(OL + OL = a\), или \(2 \cdot OL = a\).
Подставим выражение для OL: \(2 \cdot \sqrt{3} \cdot \sqrt{R^2 — \frac{a^2}{4}} = a\).
Теперь решим это уравнение относительно R.
Возведем обе части уравнения в квадрат: \((2\sqrt{3})^2 \cdot (\sqrt{R^2 — \frac{a^2}{4}})^2 = a^2\).
\(4 \cdot 3 \cdot (R^2 — \frac{a^2}{4}) = a^2\).
\(12 \cdot (R^2 — \frac{a^2}{4}) = a^2\).
Раскроем скобки: \(12R^2 — 12 \cdot \frac{a^2}{4} = a^2\).
\(12R^2 — 3a^2 = a^2\).
Перенесем \(3a^2\) в правую часть уравнения: \(12R^2 = a^2 + 3a^2\).
\(12R^2 = 4a^2\).
Разделим обе части на 12: \(R^2 = \frac{4a^2}{12}\).
\(R^2 = \frac{a^2}{3}\).
Извлечем квадратный корень из обеих частей: \(R = \sqrt{\frac{a^2}{3}}\).
\(R = \frac{\sqrt{a^2}}{\sqrt{3}} = \frac{a}{\sqrt{3}}\).
Чтобы избавиться от иррациональности в знаменателе, умножим числитель и знаменатель на \(\sqrt{3}\):
\(R = \frac{a}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{a\sqrt{3}}{3}\).
Таким образом, радиус цилиндра равен \(\frac{a\sqrt{3}}{3}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.