
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 396 Атанасян — Подробные Ответы
Площадь осевого сечения цилиндра равна S. Найдите площадь сечения цилиндра плоскостью, проходящей через середину радиуса основания перпендикулярно к этому радиусу.
Осевое сечение цилиндра представляет собой прямоугольник со сторонами, равными диаметру основания \(2r\) и высоте цилиндра \(h\). Площадь осевого сечения \(S = 2rh\).
Сечение плоскостью, проходящей через середину радиуса перпендикулярно к нему, также является прямоугольником. Одна сторона этого прямоугольника равна высоте цилиндра \(h\). Другая сторона равна длине хорды, перпендикулярной радиусу на расстоянии \(r/2\) от центра.
Рассмотрим треугольник, образованный центром основания, серединой радиуса и концом хорды. Это прямоугольный треугольник с гипотенузой, равной радиусу \(r\), и одним катетом, равным \(r/2\). Длина второго катета (половина хорды) по теореме Пифагора равна \(\sqrt{r^2 — (r/2)^2} = \sqrt{r^2 — r^2/4} = \sqrt{3r^2/4} = \frac{r\sqrt{3}}{2}\).
Длина хорды равна удвоенной длине этого катета, то есть \(2 \cdot \frac{r\sqrt{3}}{2} = r\sqrt{3}\).
Площадь нового сечения равна произведению длины хорды на высоту цилиндра: \(S_{сеч} = r\sqrt{3} \cdot h\).
Из формулы площади осевого сечения \(S = 2rh\) выразим \(rh = S/2\).
Подставим это значение в формулу площади сечения: \(S_{сеч} = (rh)\sqrt{3} = \frac{S}{2}\sqrt{3}\).
Рассмотрим осевое сечение цилиндра ABCD. Это прямоугольник, стороны которого равны диаметру основания и высоте цилиндра. Обозначим радиус основания за \(r\), а высоту цилиндра за \(h\). Тогда стороны осевого сечения равны \(2r\) и \(h\). Площадь осевого сечения \(S\) равна произведению этих сторон: \(S = 2r \cdot h\).
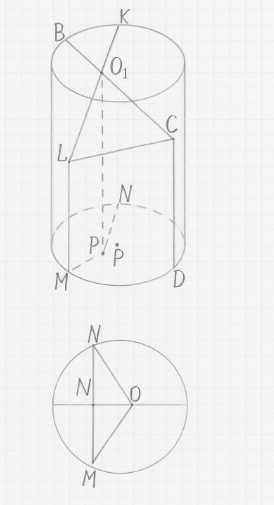
Теперь рассмотрим сечение цилиндра плоскостью MNKL. По условию, эта плоскость проходит через точку P, которая является серединой радиуса OA, и перпендикулярна к этому радиусу OA. Поскольку радиус OA лежит в плоскости основания, а плоскость MNKL перпендикулярна OA, то плоскость MNKL перпендикулярна плоскости основания. Также плоскость MNKL перпендикулярна радиусу OA, который перпендикулярен оси цилиндра. Следовательно, плоскость MNKL параллельна оси цилиндра. Сечение цилиндра плоскостью, параллельной оси, является прямоугольником.
Одна сторона этого прямоугольника MNKL равна высоте цилиндра, то есть \(LM = h\). Другая сторона равна длине хорды MN в основании цилиндра. Хорда MN перпендикулярна радиусу OA (и, следовательно, отрезку OP) и проходит через точку P на расстоянии \(OP\) от центра O. Поскольку P — середина радиуса OA, расстояние от центра O до точки P равно \(OP = \frac{OA}{2} = \frac{r}{2}\).
Рассмотрим основание цилиндра — круг с центром O и радиусом \(r\). Хорда MN перпендикулярна радиусу, проходящему через точку P. Рассмотрим прямоугольный треугольник ONP, где ON — радиус основания (\(ON = r\)), OP — расстояние от центра до хорды (\(OP = \frac{r}{2}\)), а PN — половина длины хорды MN. По теореме Пифагора в прямоугольном треугольнике ONP имеем:
\(ON^2 = OP^2 + PN^2\)
\(r^2 = \left(\frac{r}{2}\right)^2 + PN^2\)
\(r^2 = \frac{r^2}{4} + PN^2\)
\(PN^2 = r^2 — \frac{r^2}{4} = \frac{4r^2 — r^2}{4} = \frac{3r^2}{4}\)
\(PN = \sqrt{\frac{3r^2}{4}} = \frac{r\sqrt{3}}{2}\)
Длина хорды MN равна удвоенной длине отрезка PN:
\(MN = 2 \cdot PN = 2 \cdot \frac{r\sqrt{3}}{2} = r\sqrt{3}\)
Площадь сечения MNKL, которое является прямоугольником со сторонами MN и LM, равна:
\(S_{MNKL} = MN \cdot LM = r\sqrt{3} \cdot h\)
Мы знаем, что площадь осевого сечения \(S = 2rh\). Из этого соотношения выразим произведение \(rh\):
\(rh = \frac{S}{2}\)
Подставим это выражение для \(rh\) в формулу площади сечения MNKL:
\(S_{MNKL} = (rh)\sqrt{3} = \frac{S}{2}\sqrt{3}\)
Таким образом, площадь сечения цилиндра плоскостью, проходящей через середину радиуса основания перпендикулярно к этому радиусу, равна \(\frac{S}{2}\sqrt{3}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!