ГДЗ по Геометрии 10 класс Номер 395 Атанасян — Подробные Ответы

Докажите, что площадь полной поверхности цилиндра, полученного при вращении квадрата вокруг одной из его сторон, равна площади сферы, радиус которой равен стороне квадрата.

Пусть сторона квадрата равна \(a\). При вращении квадрата вокруг одной из его сторон, например стороны AB, образуется цилиндр.

Высота этого цилиндра равна стороне квадрата, то есть \(h = a\). Радиус основания цилиндра также равен стороне квадрата, то есть \(r = a\). Площадь основания цилиндра равна \(S_{осн} = \pi r^2 = \pi a^2\). Площадь боковой поверхности цилиндра равна \(S_{бок} = 2\pi r h = 2\pi a \cdot a = 2\pi a^2\). Полная площадь поверхности цилиндра складывается из площадей двух оснований и площади боковой поверхности: \(S_{полн\;цилиндра} = 2S_{осн} + S_{бок} = 2\pi a^2 + 2\pi a^2 = 4\pi a^2\). Теперь рассмотрим сферу, радиус которой равен стороне квадрата, то есть \(R = a\). Площадь поверхности сферы вычисляется по формуле \(S_{сферы} = 4\pi R^2\). Подставляя \(R = a\), получаем \(S_{сферы} = 4\pi a^2\). Таким образом, полная площадь поверхности цилиндра, полученного вращением квадрата вокруг его стороны, равна площади поверхности сферы, радиус которой равен стороне квадрата, что и требовалось доказать: \(S_{полн\;цилиндра} = S_{сферы}\).

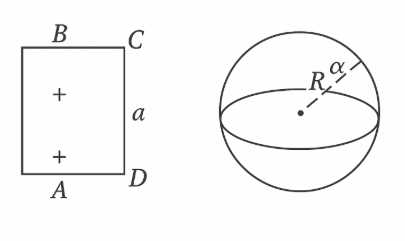
Пусть дан квадрат ABCD со стороной длиной \(a\).
Рассмотрим вращение этого квадрата вокруг одной из его сторон, например, вокруг стороны AB. При таком вращении сторона AB остается неподвижной, а стороны BC и AD описывают окружности, образующие основания цилиндра. Сторона CD описывает цилиндрическую поверхность.

В результате вращения квадрата ABCD вокруг стороны AB образуется прямой круговой цилиндр.
Высота этого цилиндра равна длине стороны, вокруг которой происходит вращение, то есть высоте квадрата. В данном случае, высота цилиндра \(h\) равна длине стороны AB, которая равна \(a\). Следовательно, \(h = a\).
Радиус основания этого цилиндра равен длине стороны квадрата, перпендикулярной оси вращения. В данном случае, это длины сторон BC или AD. Радиус цилиндра \(r\) равен длине стороны AD, которая равна \(a\). Следовательно, \(r = a\).

Теперь вычислим площадь полной поверхности полученного цилиндра.
Полная площадь поверхности цилиндра состоит из площадей двух оснований и площади боковой поверхности.
Площадь одного основания цилиндра, которое является кругом с радиусом \(r\), вычисляется по формуле \(S_{осн} = \pi r^2\). Поскольку \(r = a\), площадь одного основания равна \(S_{осн} = \pi a^2\).
Площадь двух оснований равна \(2 \cdot S_{осн} = 2 \cdot \pi a^2\).

Площадь боковой поверхности цилиндра вычисляется по формуле \(S_{бок} = 2\pi r h\). Подставляя значения радиуса \(r = a\) и высоты \(h = a\), получаем: \(S_{бок} = 2\pi (a)(a) = 2\pi a^2\).

Полная площадь поверхности цилиндра \(S_{полн\;цилиндра}\) равна сумме площадей двух оснований и площади боковой поверхности:
\(S_{полн\;цилиндра} = 2S_{осн} + S_{бок}\)
\(S_{полн\;цилиндра} = 2\pi a^2 + 2\pi a^2\)
\(S_{полн\;цилиндра} = 4\pi a^2\).

Теперь рассмотрим сферу, радиус которой равен стороне квадрата. Пусть радиус этой сферы \(R\). По условию, \(R = a\).
Площадь поверхности сферы вычисляется по формуле \(S_{сферы} = 4\pi R^2\).
Подставляя значение радиуса сферы \(R = a\), получаем:
\(S_{сферы} = 4\pi (a)^2\)
\(S_{сферы} = 4\pi a^2\).

Сравнивая полную площадь поверхности цилиндра и площадь поверхности сферы, мы видим, что:
\(S_{полн\;цилиндра} = 4\pi a^2\)
\(S_{сферы} = 4\pi a^2\)
Следовательно, \(S_{полн\;цилиндра} = S_{сферы}\).

Таким образом, площадь полной поверхности цилиндра, полученного при вращении квадрата вокруг одной из его сторон, равна площади сферы, радиус которой равен стороне квадрата. Доказательство завершено.