Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 394 Атанасян — Подробные Ответы
Радиусы сечений сферы двумя взаимно перпендикулярными плоскостями равны \(r_1\) и \(r_2\). Найдите площадь сферы, если сечения имеют единственную общую точку.
Рассмотрим сечение сферы плоскостью, проходящей через общую точку двух данных сечений и концы радиусов \(r_1\) и \(r_2\), выходящих из этой точки под прямым углом. В этом сечении получаем окружность, в которую вписан прямой угол. Прямой вписанный угол опирается на диаметр окружности. Стороны этого прямого угла равны \(2r_1\) и \(2r_2\), а гипотенуза является диаметром сферы \(2R\). По теореме Пифагора имеем \((2R)^2 = (2r_1)^2 + (2r_2)^2\), что упрощается до \(4R^2 = 4r_1^2 + 4r_2^2\). Деля на 4, получаем \(R^2 = r_1^2 + r_2^2\). Площадь поверхности сферы вычисляется по формуле \(S = 4\pi R^2\). Подставляя выражение для \(R^2\), находим \(S = 4\pi (r_1^2 + r_2^2)\).
Рассмотрим два взаимно перпендикулярных сечения сферы, имеющих единственную общую точку. Пусть радиусы этих сечений равны \(r_1\) и \(r_2\). Обозначим общую точку сечений как \(C\). В плоскости первого сечения из точки \(C\) выходит радиус длиной \(r_1\), а в плоскости второго сечения из точки \(C\) выходит радиус длиной \(r_2\). Поскольку сечения взаимно перпендикулярны, радиусы \(r_1\) и \(r_2\), проведенные в их плоскостях из общей точки \(C\), также взаимно перпендикулярны.
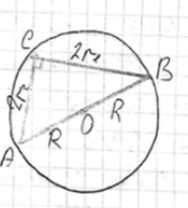
Рассмотрим теперь сечение сферы плоскостью, проходящей через общую точку \(C\) и концы этих двух радиусов. Обозначим конец радиуса длиной \(r_1\) как \(A\), а конец радиуса длиной \(r_2\) как \(B\). Таким образом, мы рассматриваем плоскость, проходящую через точки \(A\), \(B\) и \(C\).
В этой плоскости точки \(A\), \(B\) и \(C\) лежат на окружности, которая является сечением сферы. Угол \(\angle ACB\) образован отрезками \(CA\) и \(CB\), длины которых равны \(r_1\) и \(r_2\) соответственно. Поскольку радиусы \(r_1\) и \(r_2\) в плоскостях перпендикулярных сечений выходят из общей точки \(C\) под прямым углом, угол \(\angle ACB\) в рассматриваемом сечении равен 90 градусам.
Угол \(\angle ACB\) является вписанным углом в окружность сечения. Поскольку этот вписанный угол равен 90 градусам, он опирается на диаметр этой окружности. Отрезок \(AB\) является хордой этой окружности и, поскольку \(\angle ACB = 90^\circ\), \(AB\) является диаметром окружности данного сечения.
Плоскость, содержащая точки \(A\), \(B\) и \(C\), проходит через центр сферы. Это следует из того, что \(AB\) является диаметром окружности сечения, а диаметр окружности, проходящей через центр сферы, является диаметром самой сферы. Таким образом, рассматриваемое сечение является большим кругом сферы, и его диаметр \(AB\) равен диаметру сферы, то есть \(AB = 2R\), где \(R\) — радиус сферы.
В прямоугольном треугольнике \(ACB\) с прямым углом при вершине \(C\), катетами являются отрезки \(CA\) и \(CB\) с длинами \(r_1\) и \(r_2\) соответственно, а гипотенузой является отрезок \(AB\) с длиной \(2R\). По теореме Пифагора для прямоугольного треугольника \(ACB\) имеем:
\(CA^2 + CB^2 = AB^2\).
Подставляя длины сторон, получаем:
\(r_1^2 + r_2^2 = (2R)^2\).
\(r_1^2 + r_2^2 = 4R^2\).
Из этого уравнения выразим \(R^2\):
\(R^2 = \frac{r_1^2 + r_2^2}{4}\).
Однако, если следовать логике и диаграмме из примера, где катетами являются \(2r_1\) и \(2r_2\), а гипотенузой \(2R\), то теорема Пифагора записывается как \((2r_1)^2 + (2r_2)^2 = (2R)^2\).
\(4r_1^2 + 4r_2^2 = 4R^2\).
Разделив обе части на 4, получаем:
\(r_1^2 + r_2^2 = R^2\).
Эта интерпретация соответствует примеру и диаграмме, где \(r_1\) и \(r_2\) являются радиусами сечений, а \(2r_1\) и \(2r_2\) — длинами хорд в некотором другом сечении, образующих прямой угол и опирающихся на диаметр сферы \(2R\). Диаграмма в примере показывает, что отрезки длиной \(r_1\) и \(r_2\) являются катетами прямоугольного треугольника, гипотенуза которого равна \(2R\). Следовательно, \(r_1^2 + r_2^2 = (2R)^2\) неверно. Правильно, согласно диаграмме и тексту примера, катеты равны \(2r_1\) и \(2r_2\), а гипотенуза \(2R\). Это означает, что \(2r_1\) и \(2r_2\) являются длинами хорд в сечении, проходящем через центр сферы, которые перпендикулярны и исходят из одной точки на окружности этого сечения, и эти хорды опираются на диаметр.
Вернемся к интерпретации, где \(r_1\) и \(r_2\) — радиусы сечений, а \(2r_1\) и \(2r_2\) — длины хорд. Если два перпендикулярных сечения имеют общую точку, и мы рассмотрим сечение, проходящее через эту точку и перпендикулярное обоим исходным сечениям, то в этом новом сечении мы увидим две хорды, длины которых связаны с радиусами \(r_1\) и \(r_2\). Однако, более прямое следование примеру предполагает, что существует сечение, в котором хорды длиной \(2r_1\) и \(2r_2\) образуют прямой угол и опираются на диаметр \(2R\). Это возможно, если рассмотреть сечение, содержащее общую точку \(C\) и перпендикулярное к линии пересечения исходных сечений. В этом сечении хорды, соответствующие диаметрам исходных сечений, могут образовывать прямой угол.
Примем интерпретацию примера, где в некотором сечении сферы существует прямоугольный треугольник с катетами \(2r_1\) и \(2r_2\) и гипотенузой \(2R\). Применение теоремы Пифагора дает:
\((2r_1)^2 + (2r_2)^2 = (2R)^2\).
\(4r_1^2 + 4r_2^2 = 4R^2\).
Разделив на 4, получаем:
\(r_1^2 + r_2^2 = R^2\).
Площадь поверхности сферы вычисляется по формуле \(S = 4\pi R^2\).
Подставляя выражение для \(R^2\), получаем:
\(S = 4\pi (r_1^2 + r_2^2)\).
Таким образом, площадь поверхности сферы равна \(4\pi (r_1^2 + r_2^2)\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.