ГДЗ по Геометрии 10 класс Номер 387 Атанасян — Подробные Ответы

Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.

Из прямоугольного треугольника, образованного центром сферы \(O\), точкой касания \(A\) и точкой \(P\) в касательной плоскости, где \(OA\) перпендикулярно касательной плоскости, расстояние от центра сферы до точки \(P\) равно \(OP = \sqrt{OA^2 + AP^2}\). Радиус сферы \(OA = R = 112\) см, а расстояние от точки касания до точки \(P\) равно \(AP = 15\) см.
\(OP = \sqrt{112^2 + 15^2} = \sqrt{12544 + 225} = \sqrt{12769} = 113\) см.

Ближайшая к точке \(P\) точка сферы лежит на отрезке \(OP\) на расстоянии радиуса \(R\) от центра \(O\). Это точка касания \(A\). Расстояние от точки \(P\) до ближайшей точки сферы \(A\) равно разности расстояния от \(P\) до центра \(O\) и радиуса сферы:
\(AP = OP — R = 113 — 112 = 1\) см.

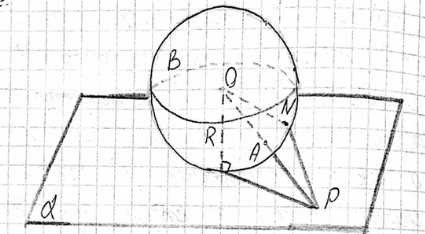
У нас есть сфера с центром в точке \(O\) и радиусом \(R\). Плоскость \(\alpha\) является касательной к сфере в точке \(A\). Точка \(P\) лежит в касательной плоскости \(\alpha\). Известно, что радиус сферы \(R = 112\) см. Расстояние от точки \(P\) до точки касания \(A\) в плоскости \(\alpha\) равно \(AP = 15\) см.

Радиус сферы, проведенный в точку касания, перпендикулярен касательной плоскости. Следовательно, отрезок \(OA\) перпендикулярен плоскости \(\alpha\). Поскольку точка \(P\) лежит в плоскости \(\alpha\), отрезок \(OA\) перпендикулярен любому отрезку в этой плоскости, выходящему из точки \(A\), включая отрезок \(AP\). Таким образом, угол между \(OA\) и \(AP\) равен \(90^\circ\).

Рассмотрим треугольник \(\triangle OAP\). Этот треугольник является прямоугольным с прямым углом при вершине \(A\). По теореме Пифагора в прямоугольном треугольнике \(\triangle OAP\) квадрат гипотенузы \(OP\) равен сумме квадратов катетов \(OA\) и \(AP\): \(OP^2 = OA^2 + AP^2\). Подставим известные значения \(OA = R = 112\) см и \(AP = 15\) см: \(OP^2 = 112^2 + 15^2 = 12544 + 225 = 12769\). Извлекаем квадратный корень, чтобы найти \(OP\): \(OP = \sqrt{12769} = 113\) см.

Ближайшая к внешней точке \(P\) точка на сфере лежит на отрезке, соединяющем эту точку \(P\) с центром сферы \(O\). Эта ближайшая точка является точкой пересечения отрезка \(OP\) со сферой, расположенной между \(O\) и \(P\). Обозначим эту ближайшую точку на сфере как \(A’\). Расстояние от центра сферы \(O\) до любой точки на сфере, включая \(A’\), равно радиусу сферы: \(OA’ = R\). Расстояние от точки \(P\) до ближайшей точки сферы \(A’\) равно разности расстояния от \(P\) до центра сферы \(O\) и радиуса сферы \(R\): \(PA’ = OP — OA’ = OP — R\). Подставим вычисленное значение \(OP = 113\) см и заданное значение \(R = 112\) см: \(PA’ = 113 — 112 = 1\) см. Таким образом, расстояние от точки \(P\) до ближайшей к ней точки сферы равно 1 см.