Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 386 Атанасян — Подробные Ответы
Сфера касается граней двугранного угла в \(120^\circ\). Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно а
Радиус сферы находится из рассмотрения сечения, перпендикулярного ребру двугранного угла, проходящего через центр сферы. В этом сечении расстояние от центра сферы до ребра равно \(a\), а угол между линиями пересечения плоскостей с этим сечением равен \(120^\circ\). Радиус сферы \(R\) связан с этим расстоянием и половиной угла между плоскостями. В прямоугольном треугольнике, образованном центром сферы, точкой касания и точкой на ребре, радиус является катетом, противолежащим углу \(60^\circ\) (половина от \(120^\circ\)), а расстояние от центра до ребра является гипотенузой. Таким образом, \(R = a \sin(60^\circ) = a \frac{\sqrt{3}}{2}\).
Расстояние между точками касания \(A\) и \(B\) равно длине отрезка \(AB\). Угол между радиусами, проведенными к точкам касания, \(\angle AOB\), связан с углом между касательными плоскостями. Если угол между плоскостями равен \(120^\circ\), то угол между нормалями к этим плоскостям (радиусами к точкам касания) равен \(180^\circ — 120^\circ = 60^\circ\). Треугольник \(AOB\) является равнобедренным с \(OA = OB = R\) и углом при вершине \(\angle AOB = 60^\circ\). Следовательно, треугольник \(AOB\) равносторонний, и расстояние между точками касания \(AB\) равно радиусу сферы \(R\). Таким образом, \(AB = R = a \frac{\sqrt{3}}{2}\).
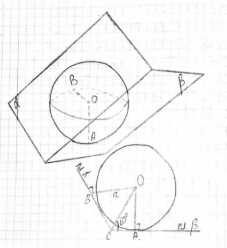
Для решения задачи рассмотрим сечение сферы и двугранного угла плоскостью, проходящей через центр сферы \(О\) и перпендикулярной ребру двугранного угла. Обозначим ребро двугранного угла как прямую \(MN\). Поскольку секущая плоскость перпендикулярна ребру \(MN\), то точка пересечения ребра \(MN\) с этой плоскостью является единственной, обозначим ее \(C\). Расстояние от центра сферы \(О\) до ребра \(MN\) по условию равно \(a\), следовательно, в секущей плоскости расстояние от точки \(О\) до точки \(C\) равно \(a\), то есть \(OC = a\).
Плоскости граней двугранного угла, обозначим их \(\alpha\) и \(\beta\), пересекают секущую плоскость по прямым. Эти прямые проходят через точку \(C\) и касаются окружности, которая является сечением сферы этой плоскостью. Обозначим точки касания сферы с гранями двугранного угла в этой секущей плоскости как \(A\) на грани \(\alpha\) и \(B\) на грани \(\beta\). Прямые \(CA\) и \(CB\) являются касательными к окружности сечения в точках \(A\) и \(B\) соответственно.
Угол между гранями двугранного угла равен \(120^\circ\). Секущая плоскость перпендикулярна ребру, поэтому угол между линиями пересечения граней с секущей плоскостью равен углу двугранного угла. Таким образом, угол между прямыми \(CA\) и \(CB\) в секущей плоскости, то есть \(\angle ACB\), равен \(120^\circ\).
Радиусы сферы, проведенные в точки касания, перпендикулярны касательным плоскостям (граням двугранного угла). В секущей плоскости радиусы \(OA\) и \(OB\), проведенные в точки касания \(A\) и \(B\), перпендикулярны касательным прямым \(CA\) и \(CB\) соответственно. Следовательно, \(\angle OAC = 90^\circ\) и \(\angle OBC = 90^\circ\).
Отрезок \(OC\) соединяет центр окружности \(О\) с точкой \(C\), из которой проведены касательные \(CA\) и \(CB\). В таком случае отрезок \(OC\) является биссектрисой угла \(\angle ACB\). Поэтому \(\angle OCA = \angle OCB = \frac{120^\circ}{2} = 60^\circ\).
Рассмотрим прямоугольный треугольник \(\triangle OAC\). Гипотенуза этого треугольника равна \(OC = a\), а катет \(OA\) является радиусом сферы, обозначим его \(R\). Угол \(\angle OCA = 60^\circ\). Используя определение синуса в прямоугольном треугольнике, получаем:
\(\sin(\angle OCA) = \frac{OA}{OC}\)
\(\sin(60^\circ) = \frac{R}{a}\)
Из этого уравнения находим радиус сферы \(R\):
\(R = a \sin(60^\circ) = a \frac{\sqrt{3}}{2}\).
Теперь найдем расстояние между точками касания \(A\) и \(B\). Рассмотрим треугольник \(\triangle AOB\). Стороны \(OA\) и \(OB\) являются радиусами сферы, поэтому \(OA = OB = R\). Угол \(\angle AOB\) можно найти из рассмотрения четырехугольника \(OACB\). Сумма углов выпуклого четырехугольника равна \(360^\circ\). У нас есть \(\angle OAC = 90^\circ\), \(\angle OBC = 90^\circ\), и \(\angle ACB = 120^\circ\).
\(\angle AOB + \angle OAC + \angle OBC + \angle ACB = 360^\circ\)
\(\angle AOB + 90^\circ + 90^\circ + 120^\circ = 360^\circ\)
\(\angle AOB + 300^\circ = 360^\circ\)
\(\angle AOB = 60^\circ\).
Треугольник \(\triangle AOB\) является равнобедренным с \(OA = OB\) и углом между равными сторонами \(\angle AOB = 60^\circ\). Равнобедренный треугольник с углом при вершине \(60^\circ\) является равносторонним. Следовательно, все стороны треугольника \(\triangle AOB\) равны: \(AB = OA = OB\).
Расстояние между точками касания \(AB\) равно радиусу сферы \(R\).
\(AB = R = a \frac{\sqrt{3}}{2}\).
Таким образом, радиус сферы равен \(a \frac{\sqrt{3}}{2}\), и расстояние между точками касания также равно \(a \frac{\sqrt{3}}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.