ГДЗ по Геометрии 10 класс Номер 385 Атанасян — Подробные Ответы

Через точку сферы радиуса R, которая является границей данного шара, проведены две плоскости, одна из которых является касательной к сфере, а другая наклонена под углом \(\phi\) к касательной плоскости. Найдите площадь сечения данного шара.

Радиус сечения шара плоскостью \(\beta\) равен \(r = R \sin \phi\). Площадь сечения шара равна \(S = \pi r^2\). Подставляя значение \(r\), получаем \(S = \pi (R \sin \phi)^2 = \pi R^2 \sin^2 \phi\).

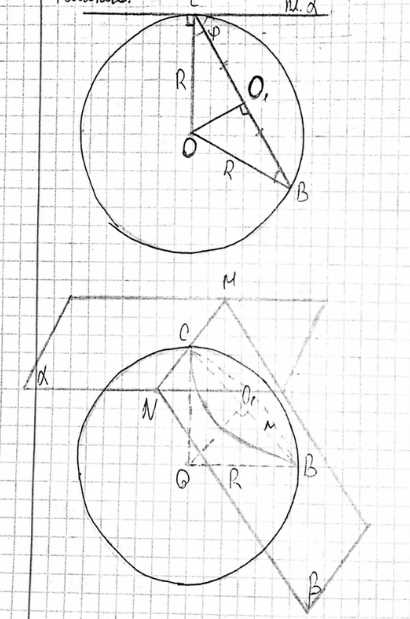
Через точку С на сфере радиуса R проведена касательная плоскость \(\alpha\). Другая плоскость \(\beta\) проходит через точку С и пересекает шар по окружности. Плоскость \(\beta\) образует с касательной плоскостью \(\alpha\) угол \(\phi\). Диаметр окружности сечения равен СВ.

Проведем радиус ОС к точке касания С. Поскольку плоскость \(\alpha\) является касательной к сфере в точке С, радиус ОС перпендикулярен плоскости \(\alpha\).

Плоскость \(\beta\) пересекает шар по окружности с диаметром СВ. Точки С и В лежат на сфере и на окружности сечения. Центр окружности сечения, обозначим его О₁, лежит на отрезке СВ.

Угол между плоскостями \(\alpha\) и \(\beta\) равен \(\phi\). Рассмотрим сечение шара плоскостью, проходящей через центр шара О и содержащей диаметр СВ. Эта плоскость перпендикулярна линии пересечения плоскостей \(\alpha\) и \(\beta\) в точке С. В этой секущей плоскости радиус ОС перпендикулярен касательной прямой, лежащей в плоскости \(\alpha\). Линия СВ лежит в плоскости \(\beta\). Угол между плоскостями \(\alpha\) и \(\beta\) равен углу между перпендикулярами к их линии пересечения в точке С. Угол между ОС (перпендикуляром к \(\alpha\)) и СВ (лежащей в \(\beta\)) связан с углом \(\phi\). Согласно условию и рисунку, угол между радиусом ОС и хордой СВ равен \(90^\circ — \phi\), то есть \(\angle OCB = 90^\circ — \phi\).

Треугольник ОСВ равнобедренный, так как ОС = ОВ = R (радиусы шара). В равнобедренном треугольнике углы при основании равны, поэтому \(\angle OCB = \angle OBC = 90^\circ — \phi\).

Центр окружности сечения О₁ лежит на диаметре СВ. Треугольник ОО₁В является прямоугольным с прямым углом при О₁, так как прямая, соединяющая центр шара с центром сечения, перпендикулярна плоскости сечения. В этом прямоугольном треугольнике гипотенуза ОВ = R (радиус шара), а катет О₁В является радиусом окружности сечения, обозначим его \(r\). Угол \(\angle OBO_1 = \angle OBC = 90^\circ — \phi\).

Используя определение косинуса в прямоугольном треугольнике ОО₁В:
\(\cos(\angle OBO_1) = \frac{O_1B}{OB}\)
\(\cos(90^\circ — \phi) = \frac{r}{R}\)

Известно, что \(\cos(90^\circ — \phi) = \sin \phi\).
Следовательно, \(\sin \phi = \frac{r}{R}\).
Отсюда находим радиус сечения: \(r = R \sin \phi\).

Площадь сечения шара плоскостью является площадью круга радиуса \(r\). Формула площади круга: \(S = \pi r^2\).
Подставляем найденное значение \(r\):
\(S = \pi (R \sin \phi)^2\)
\(S = \pi R^2 \sin^2 \phi\)

Таким образом, площадь сечения шара плоскостью \(\beta\) равна \(\pi R^2 \sin^2 \phi\).