
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 384 Атанасян — Подробные Ответы
Секущая плоскость проходит через конец диаметра сферы радиуса R так, что угол между диаметром и плоскостью равен \(\alpha\). Найдите длину окружности, получившейся в сечении, если: а) \(R = 2\) см, \(\alpha = 30^\circ\); б) \(R = 5\) м, \(\alpha = 45^\circ\).
Радиус окружности сечения определяется по формуле \(r = R \cos \alpha\). Длина окружности сечения находится как \(L = 2\pi r\). Подставляя выражение для \(r\), получаем \(L = 2\pi R \cos \alpha\).
а) При \(R = 2\) см и \(\alpha = 30^\circ\), \(L = 2\pi (2) \cos 30^\circ = 4\pi \frac{\sqrt{3}}{2} = 2\pi \sqrt{3}\) см.
б) При \(R = 5\) м и \(\alpha = 45^\circ\), \(L = 2\pi (5) \cos 45^\circ = 10\pi \frac{\sqrt{2}}{2} = 5\pi \sqrt{2}\) м.
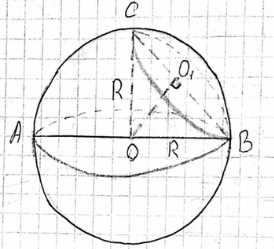
Рассмотрим сферу с центром в точке \(O\) и радиусом \(R\). Секущая плоскость проходит через точку \(B\) на поверхности сферы, которая является концом диаметра. Пусть этот диаметр лежит на прямой, проходящей через \(O\) и \(B\). Угол между этим диаметром (или радиусом \(OB\)) и секущей плоскостью равен \(\alpha\).
Сечение сферы плоскостью является окружностью. Пусть \(O_1\) — центр этой окружности, а \(r\) — ее радиус. Точка \(O_1\) лежит в секущей плоскости. Прямая \(OO_1\) перпендикулярна секущей плоскости.
Рассмотрим треугольник \(\Delta OO_1B\). Точка \(B\) лежит как на сфере, так и в секущей плоскости, поэтому \(B\) находится на окружности сечения. \(OB\) — это радиус сферы, следовательно, \(OB = R\). \(O_1B\) — это радиус окружности сечения, следовательно, \(O_1B = r\). Поскольку \(OO_1\) перпендикулярна секущей плоскости, треугольник \(\Delta OO_1B\) является прямоугольным с прямым углом при вершине \(O_1\).
Угол между радиусом \(OB\) и секущей плоскостью равен \(\alpha\). В прямоугольном треугольнике \(\Delta OO_1B\) этот угол соответствует углу \(\angle OBO_1\). Таким образом, \(\angle OBO_1 = \alpha\).
В прямоугольном треугольнике \(\Delta OO_1B\) мы можем использовать тригонометрические соотношения для связи сторон и углов. Радиус окружности сечения \(r = O_1B\) является катетом, прилежащим к углу \(\alpha\), а радиус сферы \(R = OB\) является гипотенузой. По определению косинуса, отношение прилежащего катета к гипотенузе равно косинусу угла:
\(\cos \alpha = \frac{O_1B}{OB}\)
\(\cos \alpha = \frac{r}{R}\)
Отсюда выразим радиус окружности сечения \(r\):
\(r = R \cos \alpha\)
Длина окружности сечения \(L\) вычисляется по формуле:
\(L = 2\pi r\)
Подставим выражение для \(r\) в формулу для \(L\):
\(L = 2\pi (R \cos \alpha)\)
\(L = 2\pi R \cos \alpha\)
Теперь применим эту формулу для заданных случаев:
а) Дано: \(R = 2\) см, \(\alpha = 30^\circ\).
Подставляем значения в формулу для \(L\):
\(L = 2\pi (2 \text{ см}) \cos 30^\circ\)
\(L = 4\pi \text{ см} \cdot \frac{\sqrt{3}}{2}\)
\(L = 2\pi \sqrt{3}\) см.
б) Дано: \(R = 5\) м, \(\alpha = 45^\circ\).
Подставляем значения в формулу для \(L\):
\(L = 2\pi (5 \text{ м}) \cos 45^\circ\)
\(L = 10\pi \text{ м} \cdot \frac{\sqrt{2}}{2}\)
\(L = 5\pi \sqrt{2}\) м.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!