Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 383 Атанасян — Подробные Ответы
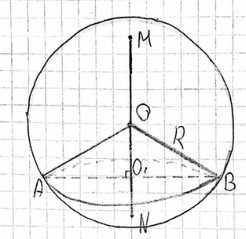
Через точку, делящую радиус сферы пополам, проведена секущая плоскость, перпендикулярная к этому радиусу. Радиус сферы равен R. Найдите: а) радиус получившегося сечения; б) площадь боковой поверхности конуса, вершиной которого является центр сферы, а основанием — полученное сечение.
Решение:
а) Радиус сечения \(r\) найдем из прямоугольного треугольника, образованного радиусом сферы \(R\), расстоянием от центра сферы до плоскости сечения \(OO_1 = \frac{R}{2}\) и радиусом сечения \(r\). По теореме Пифагора: \(r = \sqrt{R^2 — OO_1^2} = \sqrt{R^2 — (\frac{R}{2})^2} = \sqrt{R^2 — \frac{R^2}{4}} = \sqrt{\frac{3R^2}{4}} = \frac{R\sqrt{3}}{2}\).
б) Площадь боковой поверхности конуса \(S_{бок}\) с вершиной в центре сферы и основанием в виде полученного сечения найдем по формуле \(S_{бок} = \pi r L\), где \(r\) — радиус основания конуса (радиус сечения), а \(L\) — образующая конуса (радиус сферы). \(r = \frac{R\sqrt{3}}{2}\), \(L = R\). Следовательно, \(S_{бок} = \pi \cdot \frac{R\sqrt{3}}{2} \cdot R = \frac{\pi R^2\sqrt{3}}{2}\).
Решение задачи состоит из двух частей.
Сначала найдем радиус получившегося сечения. У нас есть сфера с центром в точке \(O\) и радиусом \(R\). Секущая плоскость перпендикулярна некоторому радиусу и проходит через его середину. Пусть этот радиус будет \(ON\), где \(N\) лежит на поверхности сферы. Точка \(O_1\) — это середина радиуса \(ON\), через которую проходит секущая плоскость. Расстояние от центра сферы \(O\) до плоскости сечения равно \(OO_1 = \frac{ON}{2} = \frac{R}{2}\). Сечение сферы плоскостью является окружностью с центром в точке \(O_1\). Рассмотрим любую точку \(A\) на этой окружности. Отрезок \(OA\) является радиусом сферы, то есть \(OA = R\). Отрезок \(O_1A\) является радиусом сечения, обозначим его как \(r\). Треугольник \(AOO_1\) является прямоугольным с прямым углом при вершине \(O_1\), так как плоскость сечения перпендикулярна радиусу \(ON\), а значит и отрезку \(OO_1\). По теореме Пифагора в прямоугольном треугольнике \(AOO_1\) имеем \(OA^2 = OO_1^2 + O_1A^2\), или \(R^2 = (\frac{R}{2})^2 + r^2\). Отсюда выразим \(r^2\): \(r^2 = R^2 — (\frac{R}{2})^2 = R^2 — \frac{R^2}{4} = \frac{4R^2 — R^2}{4} = \frac{3R^2}{4}\). Извлекая квадратный корень, получаем радиус сечения \(r = \sqrt{\frac{3R^2}{4}} = \frac{\sqrt{3} \cdot \sqrt{R^2}}{\sqrt{4}} = \frac{R\sqrt{3}}{2}\). Таким образом, радиус получившегося сечения равен \(r = \frac{R\sqrt{3}}{2}\).
Теперь найдем площадь боковой поверхности конуса, вершиной которого является центр сферы, а основанием — полученное сечение. Вершина конуса находится в точке \(O\) (центр сферы). Основанием конуса является круговое сечение с центром в точке \(O_1\) и радиусом \(r = \frac{R\sqrt{3}}{2}\). Образующей конуса является отрезок, соединяющий вершину конуса (точку \(O\)) с любой точкой на окружности основания (например, точка \(A\)). Длина образующей \(L\) равна расстоянию \(OA\), которое является радиусом сферы, то есть \(L = R\). Площадь боковой поверхности прямого кругового конуса вычисляется по формуле \(S_{бок} = \pi r_{основания} L_{образующая}\). В нашем случае радиус основания конуса \(r_{основания} = r = \frac{R\sqrt{3}}{2}\), а образующая конуса \(L_{образующая} = L = R\). Подставляя эти значения в формулу, получаем \(S_{бок} = \pi \cdot \frac{R\sqrt{3}}{2} \cdot R\). Умножая, находим площадь боковой поверхности конуса: \(S_{бок} = \frac{\pi R^2\sqrt{3}}{2}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.