Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 380 Атанасян — Подробные Ответы
Все стороны ромба, диагонали которого равны 15 см и 20 см, касаются сферы радиуса 10 см. Найдите расстояние от центра сферы до плоскости ромба
Центр сферы, касающейся всех сторон ромба, проецируется в центр вписанной в ромб окружности. Найдем сторону ромба с диагоналями \(d_1 = 15\) см и \(d_2 = 20\) см по формуле \(a = \frac{1}{2}\sqrt{d_1^2 + d_2^2}\). \(a = \frac{1}{2}\sqrt{15^2 + 20^2} = \frac{1}{2}\sqrt{225 + 400} = \frac{1}{2}\sqrt{625} = \frac{1}{2} \cdot 25 = 12.5\) см. Площадь ромба равна \(S = \frac{1}{2}d_1 d_2 = \frac{1}{2} \cdot 15 \cdot 20 = 150\) см². Радиус вписанной окружности \(r\) связан с площадью и стороной ромба формулой \(S = a \cdot 2r\), откуда \(r = \frac{S}{2a} = \frac{150}{2 \cdot 12.5} = \frac{150}{25} = 6\) см. Расстояние от центра сферы до плоскости ромба \(h\) можно найти по теореме Пифагора, зная радиус сферы \(R=10\) см и радиус вписанной окружности \(r=6\) см: \(h = \sqrt{R^2 — r^2} = \sqrt{10^2 — 6^2} = \sqrt{100 — 36} = \sqrt{64} = 8\) см.
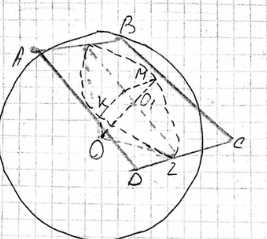
Из центра сферы О опустим перпендикуляр OO₁ на плоскость ромба ABCD. Точка O₁ является центром окружности, вписанной в ромб. Пусть радиус этой окружности равен \(r\). Радиус сферы равен \(R = 10\) см.
Рассмотрим прямоугольный треугольник, образованный центром сферы О, центром вписанной окружности O₁, и точкой касания L сферы (и вписанной окружности) со стороной ромба. В этом треугольнике OL является радиусом сферы, то есть \(OL = R = 10\) см. O₁L является радиусом вписанной окружности, то есть \(O₁L = r\). OO₁ является расстоянием от центра сферы до плоскости ромба, которое мы ищем. По теореме Пифагора имеем \(OO₁^2 + O₁L^2 = OL^2\), или \(OO₁^2 + r^2 = R^2\).
Для нахождения расстояния OO₁ необходимо вычислить радиус \(r\) вписанной в ромб окружности. Диагонали ромба равны \(d_1 = 15\) см и \(d_2 = 20\) см. Диагонали ромба взаимно перпендикулярны и делятся точкой пересечения пополам. Рассмотрим один из четырех прямоугольных треугольников, образованных половинами диагоналей. Катеты этих треугольников равны \(\frac{d_1}{2} = \frac{15}{2} = 7.5\) см и \(\frac{d_2}{2} = \frac{20}{2} = 10\) см. Гипотенуза этого треугольника является стороной ромба \(a\). По теореме Пифагора \(a^2 = (7.5)^2 + (10)^2 = 56.25 + 100 = 156.25\). Следовательно, сторона ромба \(a = \sqrt{156.25} = 12.5\) см.
Площадь ромба \(S\) может быть найдена по формуле через диагонали: \(S = \frac{1}{2} d_1 d_2 = \frac{1}{2} \cdot 15 \cdot 20 = 150\) см².
Площадь ромба также связана со стороной и радиусом вписанной окружности формулой \(S = a \cdot 2r\), поскольку \(2r\) равно высоте ромба. Отсюда радиус вписанной окружности \(r = \frac{S}{2a}\).
Подставляем значения площади и стороны: \(r = \frac{150}{2 \cdot 12.5} = \frac{150}{25} = 6\) см.
Теперь у нас есть радиус сферы \(R = 10\) см и радиус вписанной окружности \(r = 6\) см. Используем соотношение \(OO₁^2 + r^2 = R^2\) для нахождения расстояния OO₁.
\(OO₁^2 + 6^2 = 10^2\)
\(OO₁^2 + 36 = 100\)
\(OO₁^2 = 100 — 36 = 64\)
\(OO₁ = \sqrt{64} = 8\) см.
Таким образом, расстояние от центра сферы до плоскости ромба составляет 8 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.