Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
🔹 Ключевые особенности учебника:
- Структурированность — Материал разделен на четкие темы: от аксиом стереометрии до задач на векторы и координаты в пространстве. Каждая глава завершается системой упражнений разного уровня сложности.
- Баланс теории и практики — Теоретические положения иллюстрируются наглядными чертежами, а задачи подобраны так, чтобы развивать геометрическую интуицию. Например, раздел о параллельности прямых и плоскостей включает как стандартные доказательства, так и неочевидные задачи.
- Подготовка к ЕГЭ — Многие задачи (особенно в конце учебника) соответствуют формату экзамена, включая задания на построение сечений многогранников.
- Доступность языка — Даже сложные темы (например, уравнения плоскости) объясняются постепенно, с опорой на ранее изученное.
- Дополнительные материалы — В некоторых изданиях есть приложения с историческими справками (например, о Евклиде или Лобачевском), что расширяет кругозор.
🔹 Советы по использованию:
Для учеников: Начинайте изучение каждой темы с разбора примеров из учебника, а лишь затем переходите к упражнениям.
Для учителей: Учебник идеально подходит для комбинации классических уроков и проектной работы (например, построение моделей многогранников).
Для родителей: Если ребенок затрудняется, обратите внимание на раздел «Вопросы для повторения» — он помогает выявить пробелы.
Минусы (но их мало!):
Некоторым не хватает цветных иллюстраций — чертежи выполнены в черно-белой гамме.
В редких изданиях встречаются опечатки в ответах к задачам (лучше сверяться с учителем).
Вывод: Этот учебник — надежная основа для освоения геометрии. Главное — не просто решать задачи, а анализировать ход мыслей, который предлагает Атанасян. Какую тему вы считаете самой сложной? Может, стоит разобрать ее подробнее?
ГДЗ по Геометрии 10 класс Номер 378 Атанасян — Подробные Ответы
Стороны треугольника касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскости треугольника, если его стороны равны 10 см, 10 см и 12 см.
Равнобедренный треугольник PQR со сторонами 10 см, 10 см, 12 см касается сферы радиуса 5 см. Расстояние от центра сферы O до плоскости треугольника PQR равно длине перпендикуляра OO₁, где O₁ — центр вписанной окружности треугольника. Найдем радиус вписанной окружности r. Полупериметр треугольника \(p = \frac{10+10+12}{2} = 16\) см. Площадь треугольника по формуле Герона \(S = \sqrt{p(p-a)(p-b)(p-c)} =\)
\( =\sqrt{16(16-10)(16-10)(16-12)} = \sqrt{16 \cdot 6 \cdot 6 \cdot 4} = 4 \cdot 6 \cdot 2 = 48\) см². Радиус вписанной окружности \(r = \frac{S}{p} = \frac{48}{16} = 3\) см. Расстояние OO₁ можно найти по теореме Пифагора из прямоугольного треугольника OO₁B, где OB — радиус сферы \(R=5\) см, а O₁B — радиус вписанной окружности \(r=3\) см. \(OO_1 = \sqrt{R^2 — r^2} = \sqrt{5^2 — 3^2} = \sqrt{25 — 9} = \sqrt{16} = 4\) см. Расстояние от центра сферы до плоскости треугольника равно 4 см.
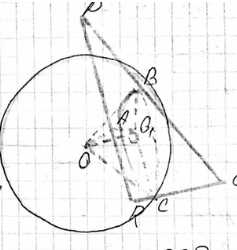
Рассмотрим равнобедренный треугольник PQR со сторонами PQ=PR=10 см и RQ=12 см. Сфера радиуса R=5 см касается всех сторон этого треугольника в точках A, B, C. Проведем перпендикуляр OO₁ из центра сферы O на плоскость треугольника PQR. Точки касания A, B, C лежат на сторонах PR, PQ, RQ соответственно. Радиусы сферы, проведенные в точки касания, перпендикулярны сторонам треугольника, то есть \(OA \perp PR\), \(OB \perp PQ\), \(OC \perp RQ\). По теореме о трех перпендикулярах, если проекция наклонной перпендикулярна прямой на плоскости, то и сама наклонная перпендикулярна этой прямой. Поскольку OA, OB, OC перпендикулярны сторонам треугольника, их проекции O₁A, O₁B, O₁C также перпендикулярны соответствующим сторонам. Это означает, что точка O₁ равноудалена от сторон треугольника PQR, а следовательно, является центром вписанной окружности треугольника.
Теперь вычислим радиус r вписанной окружности треугольника PQR. Сначала найдем полупериметр p треугольника. Стороны треугольника равны 10 см, 10 см и 12 см. Полупериметр \(p = \frac{10+10+12}{2} = \frac{32}{2} = 16\) см.
Далее вычислим площадь S треугольника PQR, используя формулу Герона: \(S = \sqrt{p(p-a)(p-b)(p-c)}\), где a, b, c — длины сторон треугольника.
\(S = \sqrt{16(16-10)(16-10)(16-12)} = \sqrt{16 \cdot 6 \cdot 6 \cdot 4}\)
\(S = \sqrt{(4^2) \cdot (6^2) \cdot (2^2)} = \sqrt{(4 \cdot 6 \cdot 2)^2} = 4 \cdot 6 \cdot 2 = 48\) см².
Радиус r вписанной окружности можно найти по формуле \(r = \frac{S}{p}\).
\(r = \frac{48}{16} = 3\) см.
У нас есть прямоугольный треугольник OO₁B, где OB — радиус сферы \(R=5\) см, O₁B — радиус вписанной окружности \(r=3\) см, и OO₁ — расстояние от центра сферы до плоскости треугольника. По теореме Пифагора в прямоугольном треугольнике OO₁B имеем \(OO_1^2 + O_1B^2 = OB^2\).
Отсюда \(OO_1^2 + r^2 = R^2\).
\(OO_1^2 = R^2 — r^2\)
\(OO_1 = \sqrt{R^2 — r^2}\)
Подставляем значения \(R=5\) см и \(r=3\) см:
\(OO_1 = \sqrt{5^2 — 3^2} = \sqrt{25 — 9} = \sqrt{16} = 4\) см.
Таким образом, расстояние от центра сферы до плоскости треугольника равно 4 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.