
Учебник Геометрия 10–11 классы авторства Л.С. Атанасяна — это классическое пособие, которое десятилетиями используется в российских школах. Он сочетает строгую логику математического изложения с доступными объяснениями, что делает его универсальным инструментом для изучения стереометрии и углубления знаний по планиметрии.
ГДЗ по Геометрии 10 класс Номер 377 Атанасян — Подробные Ответы
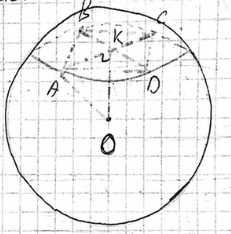
Вершины прямоугольника лежат на сфере радиуса 10 см. Найдите расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16 см.
Плоскость прямоугольника пересекает сферу по окружности, описанной около прямоугольника. Центр этой окружности находится в точке пересечения диагоналей прямоугольника, обозначим ее K. Расстояние от центра сферы O до плоскости прямоугольника равно длине отрезка OK, который перпендикулярен плоскости прямоугольника. Треугольник OKA является прямоугольным с прямым углом в K. OA — это радиус сферы, равный 10 см, то есть \(OA = R = 10\). AK — это половина диагонали прямоугольника, равной 16 см, то есть \(AK = 16 / 2 = 8\). По теореме Пифагора в прямоугольном треугольнике OKA находим OK: \(OK = \sqrt{OA^2 — AK^2} = \sqrt{10^2 — 8^2} = \sqrt{100 — 64} = \sqrt{36} = 6\). Расстояние от центра сферы до плоскости прямоугольника равно 6 см.
Дано: радиус сферы \(R = 10\) см, АВСД — прямоугольник, диагональ прямоугольника равна 16 см. Найти расстояние от центра сферы до плоскости прямоугольника.
Решение: Плоскость, в которой лежит прямоугольник АВСД, пересекает сферу. Поскольку все вершины прямоугольника лежат на сфере, линия пересечения плоскости и сферы является окружностью, которая описана около прямоугольника АВСД.
Центр окружности, описанной около прямоугольника, находится в точке пересечения его диагоналей. Обозначим эту точку К. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Таким образом, отрезок, соединяющий центр описанной окружности К с любой вершиной прямоугольника (например, А), является радиусом этой описанной окружности и равен половине длины диагонали прямоугольника.
Пусть О — центр сферы. Расстояние от центра сферы О до плоскости прямоугольника — это длина перпендикуляра, опущенного из точки О на плоскость прямоугольника. Поскольку К является центром описанной окружности, лежащей в плоскости прямоугольника, и ОА = ОВ = ОС = ОД = R (как радиусы сферы), то точка О равноудалена от всех вершин прямоугольника. Это означает, что проекция центра сферы О на плоскость прямоугольника совпадает с центром описанной окружности К. Следовательно, отрезок ОК перпендикулярен плоскости прямоугольника АВСД, и его длина является искомым расстоянием.
Рассмотрим треугольник ОКА. ОА — это радиус сферы, \(ОА = R = 10\). АК — это радиус описанной окружности, который равен половине диагонали прямоугольника. Диагональ прямоугольника равна 16 см, поэтому \(АК = 16 / 2 = 8\) см. Треугольник ОКА является прямоугольным с прямым углом при вершине К, так как ОК перпендикулярен плоскости прямоугольника.
Применим теорему Пифагора к прямоугольному треугольнику ОКА: квадрат гипотенузы ОА равен сумме квадратов катетов ОК и АК. То есть \(ОА^2 = ОК^2 + АК^2\). Из этого уравнения выразим \(ОК^2\): \(ОК^2 = ОА^2 — АК^2\). Подставим известные значения \(ОА = 10\) и \(АК = 8\): \(ОК^2 = 10^2 — 8^2\).
Вычислим значения квадратов: \(10^2 = 100\) и \(8^2 = 64\). Тогда \(ОК^2 = 100 — 64 = 36\).
Чтобы найти длину ОК, извлечем квадратный корень из 36: \(ОК = \sqrt{36}\). Поскольку длина отрезка не может быть отрицательной, берем положительное значение корня: \(ОК = 6\).
Таким образом, расстояние от центра сферы до плоскости прямоугольника равно 6 см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!